Note

Go to the end to download the full example code.

Two Ellipses Bouncing on a Wavy Street¶

Objectives¶

Show to use LineProfiler to check CPU time usage of functions.
Show different methods to find the points of least distance between two bodies with smooth contours.

Description¶

Two homogenious ellipses of semi-radii $a$ and $b$ and mass $m_e$ are dropped on an uneven street. Upon contact with the street or with each other, a force proportional to the penetration depth is applied, with spring constant $k_{\textrm{spring}}$. (That is the shapes of the bodies are not considered. This could be done with Hunt-Crossley’s method and is shown in other examples.) Also a speed dependent friction force is applied, with friction coefficient $\mu$. A particle of mass $m_o$ is placed on each ellipse.

Finding the points of least distance¶

Brute Force. Select $\textrm{accuracy}$ points on the hull of each body (e.g. $\textrm{ellipse}_0$ and $\textrm{ellipse}_1$), calculate the distance between each pair of points and select the two points with minimum distance. For $\textrm{accuracy}$ large enough, this should be close to the global minimum of the distance function. However, calculation is costly, it scales with $\textrm{accuracy}^2$.
Minimization. Use a minimization algorithm to find the minimum of the distance function. This is fast, but it may converge to a local minimum, depending on the initial guess and the distance function.
Root finding. A necessary (but not sufficient) condition for $P_0, P_1$ to be the points of least distance is that the gradient of the distance function is zero at these points. This is fast and accurate, but again it may converge to a local minimum, depending on the initial guess.

Notes¶

The distance between the two ellipses depends continuously on the the positions of the ellipses. Hence here the result of the previous time step is used as initial guess for the minimization and that result is used for root to get still more accuracy.
The distance between ellipses and the street is not continuous, hence here the brute force method is used to get an initial guess for minimization and root finding.
Any of the above only work when the bodies are not penetrating. When they do, one of the intersection points will be found. Here a trick is used: The distance to a ‘smaller’ body is calculated. If the distance is less than a certain cut-off, penetration is assumed and the penetration depth is calculated.
LineProfiler can show where the most CPU time is used in a function. it is used here on the r.h.s of the differential equations $\dot{y} = f(y, \textrm{parameters})$. It shows that brute force is the costliest operation. It may be installed with conda install conda-forge::spyder-line-profiler
symjit is a new (as of August 2025) package similar to lambdify. In this simulation it can be used for brute force and it is about twice as fast as lambdify. It may be installed with conda install conda-forge::symjit

States

$q_0, q_1$ : Angles of the ellipses
$x_0, x_1$ : x-positions of the centers of gravity of the ellipses
$y_0, y_1$ : y-positions of the centers of gravity of the ellipses
$u_0, u_1$ : Angular velocities of the ellipses
$u_{x0}, u_{x1}$ : x-velocities of the centers of gravity of the ellipses
$u_{y0}, u_{y1}$ : y-velocities of the centers of gravity of the ellipses

Parameters

$m_e$ : Mass of the ellipses
$m_o$ : Mass of the particles on the ellipses
$g$ : Gravitational acceleration
$a, b$ : Semi-radii of the ellipses
$k_{\textrm{spring}}$ : Spring constant for the contact forces
$\textrm{amplitude}, \textrm{frequenz}$ : Parameters to model the street
$\mu$ : Friction coefficient

import sympy as sm
import numpy as np
import matplotlib.pyplot as plt
import sympy.physics.mechanics as me
import itertools as itt
import time
from copy import deepcopy
from symjit import compile_func
from scipy.integrate import solve_ivp
from scipy.optimize import root, minimize
from scipy.interpolate import CubicSpline
from matplotlib.patches import Ellipse
from line_profiler import LineProfiler
from matplotlib.animation import FuncAnimation

This creates a decorator to test functions for usage of CPU time, line by line. To see the results, this line: profiler.print_stats() must be added.

profiler = LineProfiler()


def profile(func):
    def inner(*args, **kwargs):
        profiler.add_function(func)
        profiler.enable_by_count()
        return func(*args, **kwargs)
    return inner

symjit or lambdify may be used for the brute search.

choose_symjit = True

Model the street.

rumpel = 5  # the higher the number the more 'uneven the street'

amplitude, frequenz, x = sm.symbols('amplitude, frequenz, x')


def gesamt1(x, amplitude, frequenz):
    strasse = sum([amplitude/j * sm.sin(j*frequenz * x)
                   for j in range(1, rumpel)])
    strassen_form = (frequenz/2. * x)**2
    gesamt = strassen_form + strasse
    return gesamt


street_lam = sm.lambdify(
    (x, amplitude, frequenz), gesamt1(x, amplitude, frequenz), cse=True)

Geometry of the system

N, A0, A1 = sm.symbols('N A0 A1', cls=me.ReferenceFrame)
O = me.Point('O')
O.set_vel(N, 0)
t = me.dynamicsymbols._t

# Centers of gravity of the ellipses
Dmc0, Dmc1 = me.Point('Dmc0'), me.Point('Dmc1')
# Particle on the ellipses
Po0, Po1 = me.Point('Po0'), me.Point('Po1')
# Points of least distance on the ellipses
CPee0, CPee1 = me.Point('CPee0'), me.Point('CPee1')
# points of least distance on the street on the ellipses
CPes0, CPes1 = me.Point('CPes0'), me.Point('CPes1')
# Counter points on the street
CPse0, CPse1 = me.Point('CPse0'), me.Point('CPse1')

# Generalized coordinates of the ellipses
q0, q1, u0, u1, x0, x1, y0, y1, u0, u1, ux0, ux1, uy0, uy1 = me.dynamicsymbols(
    'q0 q1 u0 u1 x0 x1 y0 y1 u0 u1 ux0 ux1 uy0 uy1')

# These angles describe the points where the distances are closest
angle_ee0, angle_ee1 = sm.symbols('angle_ee0 angle_ee1')
angle_street0, angle_street1 = sm.symbols('angle_street0 angle_street1')
X0, X1 = sm.symbols('X0 X1')

# a, b are the semi axes of the ellipses
m_e, m_o, g, a, b, k_spring, mu = sm.symbols('m_e m_o g a b k_spring mu')
pen_ee, pen_se0, pen_se1 = sm.symbols('pen_ee pen_se0 pen_se1')

# Orient the frames
A0.orient_axis(N, q0, N.z)
A0.set_ang_vel(N, u0 * N.z)
A1.orient_axis(N, q1, N.z)
A1.set_ang_vel(N, u1 * N.z)

Dmc0.set_pos(O, x0 * N.x + y0 * N.y)
Dmc0.set_vel(N, ux0 * N.x + uy0 * N.y)
Dmc1.set_pos(O, x1 * N.x + y1 * N.y)
Dmc1.set_vel(N, ux1 * N.x + uy1 * N.y)
Po0.set_pos(Dmc0, a/2 * A0.x + b/2 * A0.y)
Po0.v2pt_theory(Dmc0, N, A0)
Po1.set_pos(Dmc1, a/2 * A1.x + b/2 * A1.y)
Po1.v2pt_theory(Dmc1, N, A1)

CPee0.set_pos(Dmc0, a * sm.cos(angle_ee0) * A0.x +
              b * sm.sin(angle_ee0) * A0.y)
CPee1.set_pos(Dmc1, a * sm.cos(angle_ee1) * A1.x +
              b * sm.sin(angle_ee1) * A1.y)

CPes0.set_pos(Dmc0, a * sm.cos(angle_street0) * A0.x +
              b * sm.sin(angle_street0) * A0.y)
CPes1.set_pos(Dmc1, a * sm.cos(angle_street1) * A1.x +
              b * sm.sin(angle_street1) * A1.y)

CPse0.set_pos(O, X0 * N.x + gesamt1(X0, amplitude, frequenz) * N.y)
CPse1.set_pos(O, X1 * N.x + gesamt1(X1, amplitude, frequenz) * N.y)

Set initial conditions

q01 = np.deg2rad(45)
q11 = np.deg2rad(-30)

x01 = -3.5
x11 = 5.0
y01 = 6.5
y11 = 7.0

u01 = 4.0
u11 = -4.0
ux01 = 0.0
ux11 = 0.0
uy01 = 0.0
uy11 = 0.0

m_e1 = 1.0
m_o1 = 1.0
g1 = 9.81
a1 = 1.0
b1 = 2.0
k_spring1 = 5000.0
amplitude1 = 1.0
frequenz1 = 0.5
mu1 = 0.025

accuracy = 50
safety_factor = 1.e-2

y00 = [q01, q11, x01, x11, y01, y11, u01, u11, ux01, ux11, uy01, uy11]
pL_vals = [m_e1, m_o1, g1, a1, b1, k_spring1, amplitude1, frequenz1, mu1]

Get the distance between the two ellipses in three ways. Distance must be positive, else one of the intersection points will be found.

qL = [q0, q1, x0, x1, y0, y1, u0, u1, ux0, ux1, uy0, uy1]
pL = [m_e, m_o, g, a, b, k_spring, amplitude, frequenz, mu]


Pe0, Pe1 = sm.symbols('Pe0 Pe1', cls=me.Point)
angle0, angle1 = sm.symbols('angle0 angle1')

# brute force search for minimum distance
search_space = list(itt.product(np.linspace(0, 2*np.pi, accuracy),
                                np.linspace(0, 2*np.pi, accuracy)))


def distance_func_ee(angle0, angle1):
    Pe0.set_pos(Dmc0, a * sm.cos(angle0) * A0.x + b * sm.sin(angle0) * A0.y)
    Pe1.set_pos(Dmc1, a * sm.cos(angle1) * A1.x + b * sm.sin(angle1) * A1.y)
    distance = sm.sqrt(safety_factor**2 + Pe0.pos_from(Pe1).dot(N.x)**2 +
                       Pe0.pos_from(Pe1).dot(N.y)**2)
    return distance


distance_ee_lam = sm.lambdify(([angle0, angle1] + qL + pL),
                              distance_func_ee(angle0, angle1), cse=True)

distance_array = np.array([distance_ee_lam(*([angle0, angle1] + y00 + pL_vals))
                           for angle0, angle1 in search_space])

min_distance = np.min(distance_array)
min_distance_index = np.argmin(distance_array)
angle_brute_0 = np.linspace(0, 2*np.pi, accuracy)[min_distance_index //
                                                  accuracy]
angle_brute_1 = np.linspace(0, 2*np.pi, accuracy)[min_distance_index %
                                                  accuracy]

# Search by minimizing the distance function.


def distance_minimizer(X00, args):
    angle0, angle1 = X00
    return distance_ee_lam(*([angle0, angle1] + args))


X00 = [0.0, 1.0]
args = y00 + pL_vals
loesung = minimize(distance_minimizer, X00, args, tol=1.e-6)
angle_min_0, angle_min_1 = loesung.x
print(loesung.message)

# Solve with gradient(distance) = 0


def distance_ee_grad(angle0, angle1):
    Pe0.set_pos(Dmc0, a * sm.cos(angle0) * A0.x + b * sm.sin(angle0) * A0.y)
    Pe1.set_pos(Dmc1, a * sm.cos(angle1) * A1.x + b * sm.sin(angle1) * A1.y)
    grad = [sm.sqrt(safety_factor**2 + Pe0.pos_from(Pe1).dot(N.x)**2 +
                    Pe0.pos_from(Pe1).dot(N.y)**2).diff(angle)
            for angle in (angle0, angle1)]
    return grad


distance_ee_grad_lam = sm.lambdify(([angle0, angle1] + qL + pL),
                                   distance_ee_grad(angle0, angle1), cse=True)


def equations_ee(X00, args):
    angle0, angle1 = X00
    return distance_ee_grad_lam(*([angle0, angle1] + args))


X00 = [angle_min_0, angle_min_1]
args = y00 + pL_vals
loesung = root(equations_ee, X00, args)
angle_root_0, angle_root_1 = loesung.x
print(loesung.message)

# 'Print the results to compare the three methods '
print('brute force.   Distance', min_distance, 'angle01',
      np.rad2deg(angle_brute_0), 'angle02 ', np.rad2deg(angle_brute_1))
print('minimization.  Distance', distance_ee_lam(*(loesung.x.tolist() + args)),
      'angle01', np.rad2deg(loesung.x[0]), 'angle02', np.rad2deg(loesung.x[1]))
print('root.          Distance', distance_ee_lam(*(loesung.x.tolist() + args)),
      'angle01', np.rad2deg(loesung.x[0]), 'angle02', np.rad2deg(loesung.x[1]))

Optimization terminated successfully.
The solution converged.
brute force.   Distance 5.612321571257076 angle01 301.2244897959183 angle02  235.1020408163265
minimization.  Distance 5.609102365412254 angle01 -60.7651534216529 angle02 -127.35808775141366
root.          Distance 5.609102365412254 angle01 -60.7651534216529 angle02 -127.35808775141366

Get the distance between ellipse and street in three ways. Distance must be positive, else one of the points where they intersect will be found.

If the distance gets very close to zero, numerical problems araise with minimizer and with root. safety_factor is used so the argument in sqrt remains positive at all times.

Pe0, Pe1 = sm.symbols('Pe0 Pe1', cls=me.Point)
street_point, angle_street = sm.symbols('street_point angle_street')
grenze = 25.0

# brute force search for minimum distance
search_space = list(itt.product(np.linspace(-grenze, grenze, accuracy),
                                np.linspace(0, 2*np.pi, accuracy)))


def distance_func0(street_point, angle_street):
    Pe0, Pe1 = sm.symbols('Pe0 Pe1', cls=me.Point)
    Pe0.set_pos(Dmc0, a * sm.cos(angle_street) * A0.x +
                b * sm.sin(angle_street) * A0.y)
    Pe1.set_pos(O, street_point * N.x + gesamt1(street_point,
                                                amplitude, frequenz) * N.y)
    distance = sm.sqrt(safety_factor**2 + (Pe0.pos_from(Pe1).dot(N.x))**2 +
                       (Pe0.pos_from(Pe1).dot(N.y))**2)
    return distance


def distance_func1(street_point, angle_street):
    Pe0, Pe1 = sm.symbols('Pe0 Pe1', cls=me.Point)
    Pe0.set_pos(Dmc1, a * sm.cos(angle_street) * A1.x +
                b * sm.sin(angle_street) * A1.y)
    Pe1.set_pos(O, street_point * N.x + gesamt1(street_point,
                                                amplitude, frequenz) * N.y)

    distance = sm.sqrt(safety_factor**2 + (Pe0.pos_from(Pe1).dot(N.x))**2 +
                       (Pe0.pos_from(Pe1).dot(N.y))**2)
    return distance


if not choose_symjit:
    distance_lam = sm.lambdify(([street_point, angle_street] + qL + pL),
                               [distance_func0(street_point, angle_street),
                                distance_func1(street_point, angle_street)],
                               cse=True)
else:
    helpers = [sm.symbols('helper'+str(i)) for i in range(len(qL))]
    dict_qL = {qL[i]: helpers[i] for i in range(len(qL))}
    args_ufunc = tuple([street_point, angle_street] + helpers + pL)
    distance_lam = compile_func(
        (args_ufunc), (distance_func0(street_point,
                                      angle_street).subs(dict_qL),
                       distance_func1(street_point,
                                      angle_street).subs(dict_qL)))
ellipse_street_brute = []
ellipse_street_min = []
ellipse_street_root = []

for i in range(2):
    distance_array = np.array(
        [distance_lam(*([street_point, angle_street] + y00 + pL_vals))[i]
         for street_point, angle_street in search_space])

    min_distance = np.min(distance_array)
    min_distance_index = np.argmin(distance_array)
    street_point_brute = np.linspace(
        -grenze, grenze, accuracy)[min_distance_index // accuracy]
    angle_street_brute = np.linspace(
        0, 2*np.pi, accuracy)[min_distance_index % accuracy]
    ellipse_street_brute.append([street_point_brute, angle_street_brute])

    # Search by minimizing the distance function.
    def distance_minimizer(X00, args):
        street_point, angle_street = X00
        return distance_lam(*([street_point, angle_street] + args))[i]

    X00 = [0.0, 1.0]
    args = y00 + pL_vals
    loesung = minimize(distance_minimizer, X00, args, tol=1.e-6)
    street_point_min, angle_street_min = loesung.x
    print(loesung.message)
    ellipse_street_min.append([street_point_min, angle_street_min])

# Solve with gradient(distance) = 0


def distance_grad0(street_point, angle_street):
    Pe0, Pe1 = sm.symbols('Pe0 Pe1', cls=me.Point)
    Pe0.set_pos(Dmc0, a * sm.cos(angle_street) * A0.x +
                b * sm.sin(angle_street) * A0.y)
    Pe1.set_pos(O, street_point * N.x + gesamt1(street_point,
                                                amplitude, frequenz) * N.y)
    grad = [sm.sqrt(safety_factor**2 + Pe0.pos_from(Pe1).dot(N.x)**2 +
                    Pe0.pos_from(Pe1).dot(N.y)**2).diff(angle)
            for angle in (street_point, angle_street)]
    return grad


def distance_grad1(street_point, angle_street):
    Pe0, Pe1 = sm.symbols('Pe0 Pe1', cls=me.Point)
    Pe0.set_pos(Dmc1, a * sm.cos(angle_street) * A1.x +
                b * sm.sin(angle_street) * A1.y)
    Pe1.set_pos(O, street_point * N.x + gesamt1(street_point,
                                                amplitude, frequenz) * N.y)
    grad = [sm.sqrt(safety_factor**2 + (Pe0.pos_from(Pe1).dot(N.x))**2 +
                    (Pe0.pos_from(Pe1).dot(N.y))**2).diff(angle)
            for angle in (street_point, angle_street)]
    return grad


distance_grad_lam = sm.lambdify(([street_point, angle_street] + qL + pL),
                                [distance_grad0(street_point, angle_street),
                                 distance_grad1(street_point, angle_street)],
                                cse=True)

for i in range(2):
    def equations(X00, args):
        street_point, angle_street = X00
        return distance_grad_lam(*([street_point, angle_street] + args))[i]

    X00 = [ellipse_street_min[i][0], ellipse_street_min[i][1]]
    args = y00 + pL_vals
    loesung = root(equations, X00, args, method='hybr')
    street_point_root, angle_street_root = loesung.x
    print(loesung.message)
    ellipse_street_root.append([street_point_root, angle_street_root])

print('\n')
print(f"{' ' * 5} street point angles01{' ' * 25} street point angles02")
print('brute', ellipse_street_brute)
print('min', ellipse_street_min)
print('root', ellipse_street_root, '\n')

print(f'{" " * 5} Distance ellipse0 / street{" " * 10} ellipse1 / street')
print('Brute method:', distance_lam(*(ellipse_street_brute[0] + y00 +
                                      pL_vals))[0], f"{' ' * 12}",
      distance_lam(*(ellipse_street_brute[1] + y00 + pL_vals))[1])
print('Minimization:', distance_lam(*(ellipse_street_min[0] + y00 +
                                      pL_vals))[0], f"{' ' * 12}",
      distance_lam(*(ellipse_street_min[1] + y00 + pL_vals))[1])
print('Root method :', distance_lam(*(ellipse_street_root[0] + y00 +
                                      pL_vals))[0], f"{' ' * 12}",
      distance_lam(*(ellipse_street_root[1] + y00 + pL_vals))[1])


def distance_se0(street_point, angle_street):
    Pe0, Pe1 = sm.symbols('Pe0 Pe1', cls=me.Point)
    Pe0.set_pos(Dmc0, a * sm.cos(angle_street) * A0.x +
                b * sm.sin(angle_street) * A0.y)
    Pe1.set_pos(O, street_point * N.x + gesamt1(street_point,
                                                amplitude, frequenz) * N.y)

    distance = sm.sqrt(safety_factor**2 + (Pe0.pos_from(Pe1).dot(N.x))**2 +
                       (Pe0.pos_from(Pe1).dot(N.y))**2)
    return distance


# Needed for some plotting


def distance_se1(street_point, angle_street):
    Pe0, Pe1 = sm.symbols('Pe0 Pe1', cls=me.Point)
    Pe0.set_pos(Dmc1, a * sm.cos(angle_street) * A1.x +
                b * sm.sin(angle_street) * A1.y)
    Pe1.set_pos(O, street_point * N.x + gesamt1(street_point,
                                                amplitude, frequenz) * N.y)

    distance = sm.sqrt(safety_factor**2 + (Pe0.pos_from(Pe1).dot(N.x))**2 +
                       (Pe0.pos_from(Pe1).dot(N.y))**2)
    return distance


angle0, angle1 = sm.symbols('angle0 angle1')


def distance_ee(angle0, angle1):
    Pe0, Pe1 = sm.symbols('Pe0 Pe1', cls=me.Point)
    Pe0.set_pos(Dmc0, a * sm.cos(angle0) * A0.x + b * sm.sin(angle0) * A0.y)
    Pe1.set_pos(Dmc1, a * sm.cos(angle1) * A1.x + b * sm.sin(angle1) * A1.y)
    distance = sm.sqrt(safety_factor**2 + Pe0.pos_from(Pe1).dot(N.x)**2 +
                       Pe0.pos_from(Pe1).dot(N.y)**2)
    return distance


dist_se0_lam = sm.lambdify(([street_point, angle_street] + qL + pL),
                           distance_se0(street_point, angle_street), cse=True)
dist_se1_lam = sm.lambdify(([street_point, angle_street] + qL + pL),
                           distance_se1(street_point, angle_street), cse=True)
dist_ee_lam = sm.lambdify(([angle0, angle1] + qL + pL),
                          distance_ee(angle0, angle1), cse=True)

Optimization terminated successfully.
Optimization terminated successfully.
The solution converged.
The solution converged.


      street point angles01                          street point angles02
brute [[np.float64(-7.653061224489797), np.float64(2.821021974652059)], [np.float64(6.632653061224492), np.float64(5.513815677729024)]]
min [[np.float64(0.9132003078523524), np.float64(-1.6136747450923836)], [np.float64(4.665630233442586), np.float64(-1.229539128485044)]]
root [[np.float64(0.9132003163761305), np.float64(-1.6136747285217004)], [np.float64(4.665630131256732), np.float64(-1.229538948998549)]]

      Distance ellipse0 / street           ellipse1 / street
Brute method: 3.793499732740891              3.189722871620561
Minimization: 4.705442356708569              3.3890251605755863
Root method : 4.705442356708568              3.3890251605755446

Calculate the scalar product of the two normal vectors, ellipse / ellipse and ellipse / street.

A necessary condition for the distance points (but by no means sufficient) is that the normal vectors to the surfaces of the two bodies be parallel. This is checked here.

Ellipse / Ellipse

def scalar_product_ee(angle0, angle1):
    n0 = (sm.cos(angle0) * A0.x / a + sm.sin(angle0) * A0.y / b).normalize()
    n1 = (sm.cos(angle1) * A1.x / a + sm.sin(angle1) * A1.y / b).normalize()
    return n0.dot(n1)


scalar_ee_lam = sm.lambdify(
    ([angle0, angle1] + qL + pL), scalar_product_ee(angle0, angle1), cse=True)

names = ['brute', 'min', 'root']
for j, angles in enumerate(
    [(angle_brute_0, angle_brute_1), (angle_min_0, angle_min_1),
     (angle_root_0, angle_root_1)]):
    scalar = scalar_ee_lam(*(list(angles) + y00 + pL_vals))
    print(f'{names[j]} method: inner product ellipse / ellipse', scalar)


# Ellipse / street


def scalar_product_es0(street_point, angle_street):
    n_ellipse = (sm.cos(angle_street) * A0.x / a +
                 sm.sin(angle_street) * A0.y / b).normalize()
    tangent_street = (-gesamt1(street_point, amplitude, frequenz).diff(
        street_point) * N.x + N.y).normalize()
    return n_ellipse.dot(tangent_street)


def scalar_product_es1(street_point, angle_street):
    n_ellipse = (sm.cos(angle_street) * A1.x / a +
                 sm.sin(angle_street) * A1.y / b).normalize()
    tangent_street = (-gesamt1(street_point, amplitude, frequenz).diff(
        street_point) * N.x + N.y).normalize()
    return n_ellipse.dot(tangent_street)


scalar_es_lam = sm.lambdify(
    ([street_point, angle_street] + qL + pL),
    [scalar_product_es0(street_point, angle_street),
     scalar_product_es1(street_point, angle_street)], cse=True)
print('\n')
for i in range(2):
    for j, angles in enumerate([
        (ellipse_street_brute[i][0], ellipse_street_brute[i][1]),
        (ellipse_street_min[i][0], ellipse_street_min[i][1]),
        (ellipse_street_root[i][0], ellipse_street_root[i][1])]):

        scalar = scalar_es_lam(*(list(angles) + y00 + pL_vals))[i]
        print(f'{names[j]} method: inner product ellipse{i} / street', scalar)

brute method: inner product ellipse / ellipse -0.9999966468889012
min method: inner product ellipse / ellipse -0.9999999999996061
root method: inner product ellipse / ellipse -1.0000000000000002


brute method: inner product ellipse0 / street -0.9997114565375054
min method: inner product ellipse0 / street -0.999999999999999
root method: inner product ellipse0 / street -1.0000000000000002
brute method: inner product ellipse1 / street -0.9986835527376923
min method: inner product ellipse1 / street -0.9999999999999677
root method: inner product ellipse1 / street -0.9999999999999999

Penetration depth.

Here a trick is used: If the distance is less than cut_off, penetration is assumed. In other words, the distance to a ‘smaller’ body is calculated.

# Ellipse / ellipse penetration depth
cut_off = 0.4


def penetration_ee(angle0, angle1):
    Pe, Pj = sm.symbols('Pe Pj', cls=me.Point)
    Pe.set_pos(Dmc0, a * sm.cos(angle0) * A0.x + b * sm.sin(angle0) * A0.y)
    Pj.set_pos(Dmc1, a * sm.cos(angle1) * A1.x + b * sm.sin(angle1) * A1.y)
    distance = sm.sqrt(safety_factor**2 + Pe.pos_from(Pj).dot(N.x)**2 +
                       Pe.pos_from(Pj).dot(N.y)**2)
    factor = sm.Piecewise((1, distance - cut_off < 0), (0, True))
    penetration = factor * (cut_off - distance)
    return penetration


def penetration_es0(street_point, angle_street):
    Pe0, Pe1 = sm.symbols('Pe0 Pe1', cls=me.Point)
    Pe0.set_pos(Dmc0, a * sm.cos(angle_street) * A0.x +
                b * sm.sin(angle_street) * A0.y)
    Pe1.set_pos(O, street_point * N.x + gesamt1(street_point,
                                                amplitude, frequenz) * N.y)
    distance = sm.sqrt(safety_factor**2 + Pe0.pos_from(Pe1).dot(N.x)**2 +
                       Pe0.pos_from(Pe1).dot(N.y)**2)
    factor = sm.Piecewise((1, distance - cut_off < 0), (0, True))
    penetration = factor * (cut_off - distance)
    return penetration


def penetration_es1(street_point, angle_street):
    Pe0, Pe1 = sm.symbols('Pe0 Pe1', cls=me.Point)
    Pe0.set_pos(Dmc1, a * sm.cos(angle_street) * A1.x +
                b * sm.sin(angle_street) * A1.y)
    Pe1.set_pos(O, street_point * N.x + gesamt1(street_point,
                                                amplitude, frequenz) * N.y)
    distance = sm.sqrt(safety_factor**2 + Pe0.pos_from(Pe1).dot(N.x)**2 +
                       Pe0.pos_from(Pe1).dot(N.y)**2)
    factor = sm.Piecewise((1, distance - cut_off <= 0), (0, True))
    penetration = factor * (cut_off - distance)
    return penetration


pen_es_lam0 = sm.lambdify(
    ([street_point, angle_street] + qL + pL),
    penetration_es0(street_point, angle_street), cse=True)

pen_es_lam1 = sm.lambdify(
    ([street_point, angle_street] + qL + pL),
    penetration_es1(street_point, angle_street), cse=True)

pen_ee_lam = sm.lambdify(([angle0, angle1] + qL + pL),
                         penetration_ee(angle0, angle1), cse=True)

for j, angles in enumerate(
    [(angle_brute_0, angle_brute_1), (angle_min_0, angle_min_1),
     (angle_root_0, angle_root_1)]):
    pen = pen_ee_lam(*(list(angles) + y00 + pL_vals))
    print(f'{names[j]} method: penetration depth ellipse / ellipse', pen)

print('\n')
for i in range(2):
    for j, angles in enumerate(
        [(ellipse_street_brute[i][0], ellipse_street_brute[i][1]),
         (ellipse_street_min[i][0], ellipse_street_min[i][1]),
         (ellipse_street_root[i][0], ellipse_street_root[i][1])]):
        pen = [pen_es_lam0, pen_es_lam1][i](*(list(angles) + y00 + pL_vals))
        print(f'{names[j]} method: penetration depth ellipse{i} / street', pen)

brute method: penetration depth ellipse / ellipse -0.0
min method: penetration depth ellipse / ellipse -0.0
root method: penetration depth ellipse / ellipse -0.0


brute method: penetration depth ellipse0 / street -0.0
min method: penetration depth ellipse0 / street -0.0
root method: penetration depth ellipse0 / street -0.0
brute method: penetration depth ellipse1 / street -0.0
min method: penetration depth ellipse1 / street -0.0
root method: penetration depth ellipse1 / street -0.0

Forces acting on the ellipses, due to elasticity (Spring)

def force_ee(angle0, pen_ee):
    n0 = (sm.cos(angle0) * A0.x / a + sm.sin(angle0) * A0.y / b).normalize()
    f_Nx = k_spring * pen_ee * n0.dot(N.x)
    f_Ny = k_spring * pen_ee * n0.dot(N.y)
    return f_Nx, f_Ny


def force_es0(X0, pen_se0):
    no = (-gesamt1(X0, amplitude, frequenz).diff(
        X0) * N.x + N.y).normalize()
    f_Nx = k_spring * pen_se0 * no.dot(N.x)
    f_Ny = k_spring * pen_se0 * no.dot(N.y)
    return f_Nx, f_Ny


def force_es1(X1, pen_se1):
    no = (-gesamt1(X1, amplitude, frequenz).diff(
        X1) * N.x + N.y).normalize()
    f_Nx = k_spring * pen_se1 * no.dot(N.x)
    f_Ny = k_spring * pen_se1 * no.dot(N.y)
    return f_Nx, f_Ny

Force due to speed dependent friction

def force_ee_friction(angle0, angle1, pen_ee):
    Pe, Pj = sm.symbols('Pe Pj', cls=me.Point)
    Pe.set_pos(Dmc0, a * sm.cos(angle0) * A0.x + b * sm.sin(angle0) * A0.y)
    Pj.set_pos(Dmc1, a * sm.cos(angle1) * A1.x + b * sm.sin(angle1) * A1.y)
    rel_speed = Pe.vel(N) - Pj.vel(N)
    n0 = (sm.cos(angle0) * A0.x / a + sm.sin(angle0) * A0.y / b).normalize()
    force_x, force_y = force_ee(angle0, pen_ee)
    force_abs = sm.sqrt(force_x**2 + force_y**2)
    n_force = n0.cross(N.z)
    rel_speed_tangent = rel_speed.dot(n_force)
    # safety:
    factor = sm.Piecewise((1, pen_ee > 0), (0, True))
    friction_force = mu * force_abs * rel_speed_tangent * n_force * factor
    return friction_force.dot(N.x), friction_force.dot(N.y)


def force_es0_friction(X0, angle_street, pen_se0):
    Pe0, Pe1 = sm.symbols('Pe0 Pe1', cls=me.Point)
    Pe0.set_pos(Dmc0, a * sm.cos(angle_street) * A0.x +
                b * sm.sin(angle_street) * A0.y)
    Pe1.set_pos(O, X0 * N.x + gesamt1(X0, amplitude, frequenz) * N.y)
    rel_speed = Pe0.vel(N)
    no = (-gesamt1(X0, amplitude, frequenz).diff(
        X0) * N.x + N.y).normalize()
    force_x, force_y = force_es0(X0, pen_se0)
    force_abs = sm.sqrt(force_x**2 + force_y**2)
    n_force = no.cross(N.z)
    rel_speed_tangent = rel_speed.dot(n_force)
    # safety:
    factor = sm.Piecewise((1, pen_se0 > 0), (0, True))
    friction_force = -mu * force_abs * rel_speed_tangent * n_force * factor
    return friction_force.dot(N.x), friction_force.dot(N.y)


def force_es1_friction(X1, angle_street, pen_se1):
    Pe0, Pe1 = sm.symbols('Pe0 Pe1', cls=me.Point)
    Pe0.set_pos(Dmc1, a * sm.cos(angle_street) * A1.x +
                b * sm.sin(angle_street) * A1.y)
    Pe1.set_pos(O, X1 * N.x + gesamt1(X1, amplitude, frequenz) * N.y)
    rel_speed = Pe0.vel(N)
    no = (-gesamt1(X1, amplitude, frequenz).diff(
        X1) * N.x + N.y).normalize()
    force_x, force_y = force_es1(X1, pen_se1)
    force_abs = sm.sqrt(force_x**2 + force_y**2)
    n_force = no.cross(N.z)
    rel_speed_tangent = rel_speed.dot(n_force)
    # safety:
    factor = sm.Piecewise((1, pen_se1 > 0), (0, True))
    friction_force = -mu * force_abs * rel_speed_tangent * n_force * factor
    return friction_force.dot(N.x), friction_force.dot(N.y)

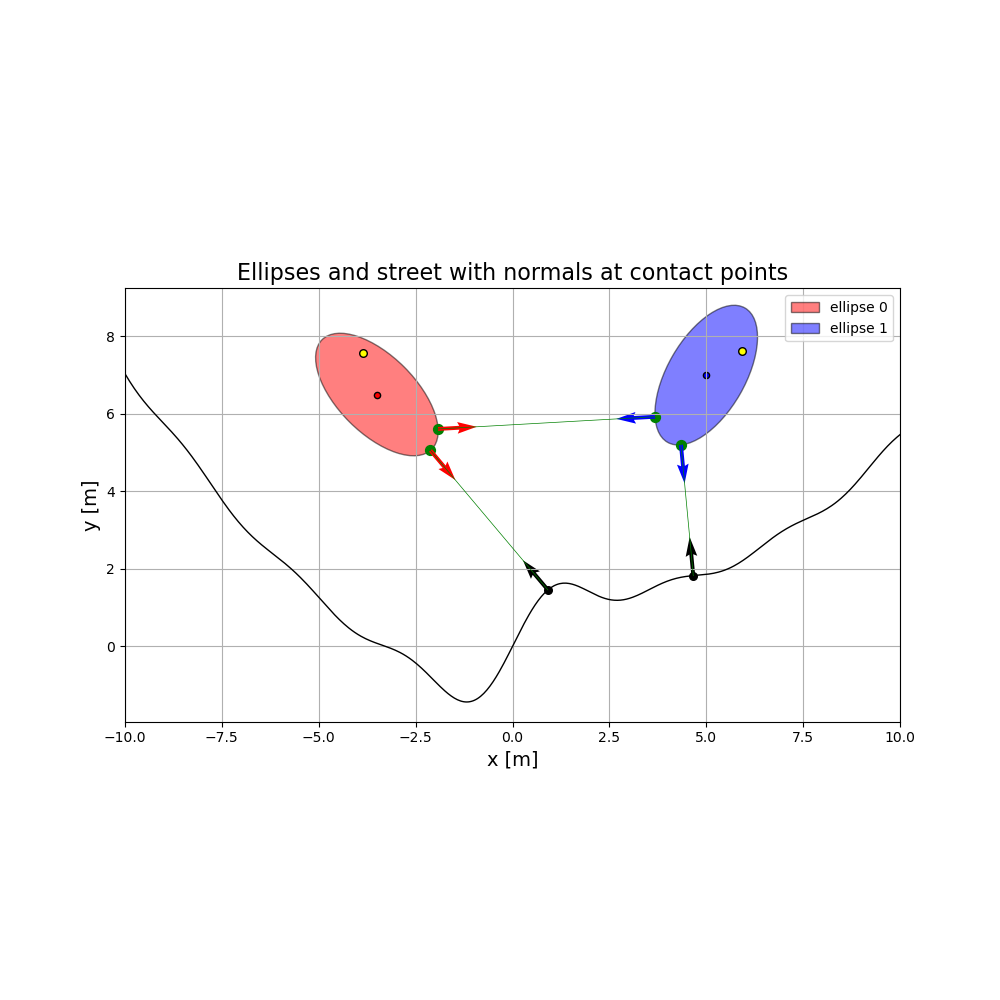
Plot the initial configuration.

# Ellipse / Ellipse
angle0_used, angle1_used = sm.symbols('angle0_used angle1_used')
arrow_ee0, arrow_ee1 = sm.symbols('arrow_ee0 arrow_ee1', cls=me.Point)

arrow_ee0.set_pos(CPee0, sm.cos(angle_ee0) * A0.x / a +
                  sm.sin(angle_ee0) * A0.y / b)
arrow_ee1.set_pos(CPee1, sm.cos(angle_ee1) * A1.x / a +
                  sm.sin(angle_ee1) * A1.y / b)

# Set the coordinates
coordinates = Dmc0.pos_from(O).to_matrix(N)
for point in (Dmc1, Po0, Po1, CPee0, CPee1, arrow_ee0, arrow_ee1):
    coordinates = coordinates.row_join(point.pos_from(O).to_matrix(N))


coords_lam = sm.lambdify((qL + pL + [angle_ee0, angle_ee1]),
                         coordinates, cse=True)

angle0_used_val = angle_root_0
angle1_used_val = angle_root_1
coords = coords_lam(*(y00 + pL_vals + [angle0_used_val, angle1_used_val]))

# Street / ellipse
street_point_used, angle_street_used = sm.symbols(
    'street_point_used angle_street_used')

arrow_es0, arrow_es1 = sm.symbols('arrow_es0 arrow_es1', cls=me.Point)
arrow_se0, arrow_se1 = sm.symbols('arrow_se0 arrow_se1', cls=me.Point)

arrow_es0.set_pos(CPes0, sm.cos(angle_street0) * A0.x / a +
                  sm.sin(angle_street0) * A0.y / b)
arrow_es1.set_pos(CPes1, sm.cos(angle_street1) * A1.x / a +
                  sm.sin(angle_street1) * A1.y / b)

arrow_se0.set_pos(
    CPse0, -gesamt1(X0, amplitude, frequenz).diff(X0) * N.x + N.y)
arrow_se1.set_pos(CPse1, -gesamt1(
    X1, amplitude, frequenz).diff(X1) * N.x + N.y)

coordinates = CPes0.pos_from(O).to_matrix(N)
for point in (CPes1, CPse0, CPse1, arrow_es0, arrow_es1, arrow_se0, arrow_se1):
    coordinates = coordinates.row_join(point.pos_from(O).to_matrix(N))

coords_es_lam = sm.lambdify((qL + pL + [angle_street0, angle_street1, X0, X1]),
                            coordinates, cse=True)

angle_street0_used_val = ellipse_street_root[0][1]
angle_street1_used_val = ellipse_street_root[1][1]
X0_used_val = ellipse_street_root[0][0]
X1_used_val = ellipse_street_root[1][0]

coords_es = coords_es_lam(
    *(y00 + pL_vals + [angle_street0_used_val, angle_street1_used_val,
                       X0_used_val, X1_used_val]))

fig, ax = plt.subplots(figsize=(10, 10))
ax.set_aspect('equal')

ellipse1 = Ellipse(
    (coords[0, 0], coords[1, 0]), width=2*a1, height=2*b1,
    angle=np.rad2deg(y00[0]), facecolor='red',
    edgecolor='black', label=f'ellipse 0', alpha=0.5)
ax.add_patch(ellipse1)

ellipse2 = Ellipse(
    (coords[0, 1], coords[1, 1]), width=2*a1, height=2*b1,
    angle=np.rad2deg(y00[1]), edgecolor='black',
    facecolor='blue', alpha=0.5, label=f'ellipse 1')
ax.add_patch(ellipse2)

# centers of the ellipses
ax.scatter([coords[0, 0]], [coords[1, 0]], color='red', edgecolors='black',
           s=20)
ax.scatter([coords[0, 1]], [coords[1, 1]], color='blue', edgecolors='black',
           s=20)
# particles on the ellipses
ax.scatter([coords[0, 2]], [coords[1, 2]], color='yellow', s=30,
           edgecolors='black')
ax.scatter([coords[0, 3]], [coords[1, 3]], color='yellow', s=30,
           edgecolors='black')

# points of least distance on the ellipses
ax.scatter([coords[0, 4]], [coords[1, 4]], color='green', s=50)
ax.scatter([coords[0, 5]], [coords[1, 5]], color='green', s=50)

# line connecting the points of least distance
ax.plot([coords[0, 4], coords[0, 5]], [coords[1, 4], coords[1, 5]],
        color='green', linestyle='-', linewidth=0.5)

# normal vectors at the points of least distance
scala = 1.0 / (np.sqrt((coords[0, 6] - coords[0, 4])**2 +
                       (coords[1, 6] - coords[1, 4])**2))
ax.quiver(coords[0, 4], coords[1, 4], scala * (coords[0, 6] - coords[0, 4]),
          scala * (coords[1, 6] - coords[1, 4]),
          color='red', angles='xy', scale_units='xy', scale=1, width=0.005)

scala = 1.0 / (np.sqrt((coords[0, 7] - coords[0, 5])**2 +
                       (coords[1, 7] - coords[1, 5])**2))
ax.quiver(coords[0, 5], coords[1, 5], scala * (coords[0, 7] - coords[0, 5]),
          scala * (coords[1, 7] - coords[1, 5]),
          color='blue', angles='xy', scale_units='xy', scale=1, width=0.005)
ax.legend()

# Draw the street
grenze = 10
x_street = np.linspace(-grenze, grenze, 500)
y_street = street_lam(x_street, amplitude1, frequenz1)
ax.plot(x_street, y_street, color='black', linestyle='-', linewidth=1)

# Draw the ellipse / street points
ax.scatter([coords_es[0, 0]], [coords_es[1, 0]], color='green', s=50)
ax.scatter([coords_es[0, 1]], [coords_es[1, 1]], color='green', s=50)
ax.scatter([coords_es[0, 2]], [coords_es[1, 2]], color='black', s=30)
ax.scatter([coords_es[0, 3]], [coords_es[1, 3]], color='black', s=30)
# line connecting the points of least distance
ax.plot([coords_es[0, 0], coords_es[0, 2]], [coords_es[1, 0], coords_es[1, 2]],
        color='green', linestyle='-', linewidth=0.5)
ax.plot([coords_es[0, 1], coords_es[0, 3]], [coords_es[1, 1], coords_es[1, 3]],
        color='green', linestyle='-', linewidth=0.5)

# Draw the normals on the ellipses
scala = 1.0 / (np.sqrt((coords_es[0, 4] - coords_es[0, 0])**2 +
                       (coords_es[1, 4] - coords_es[1, 0])**2))
ax.quiver(coords_es[0, 0], coords_es[1, 0],
          scala * (coords_es[0, 4] - coords_es[0, 0]),
          scala * (coords_es[1, 4] - coords_es[1, 0]),
          color='red', angles='xy', scale_units='xy', scale=1, width=0.005)
scala = 1.0 / (np.sqrt((coords_es[0, 5] - coords_es[0, 1])**2 +
                       (coords_es[1, 5] - coords_es[1, 1])**2))
ax.quiver(coords_es[0, 1], coords_es[1, 1],
          scala * (coords_es[0, 5] - coords_es[0, 1]),
          scala * (coords_es[1, 5] - coords_es[1, 1]),
          color='blue', angles='xy', scale_units='xy', scale=1, width=0.005)
scala = 1.0 / (np.sqrt((coords_es[0, 6] - coords_es[0, 2])**2 +
                       (coords_es[1, 6] - coords_es[1, 2])**2))
ax.quiver(coords_es[0, 2], coords_es[1, 2],
          scala * (coords_es[0, 6] - coords_es[0, 2]),
          scala * (coords_es[1, 6] - coords_es[1, 2]),
          color='black', angles='xy', scale_units='xy', scale=1, width=0.005)
scala = 1.0 / (np.sqrt((coords_es[0, 7] - coords_es[0, 3])**2 +
                       (coords_es[1, 7] - coords_es[1, 3])**2))
ax.quiver(coords_es[0, 3], coords_es[1, 3],
          scala * (coords_es[0, 7] - coords_es[0, 3]),
          scala * (coords_es[1, 7] - coords_es[1, 3]),
          color='black', angles='xy', scale_units='xy', scale=1, width=0.005)
ax.set_xlim(-grenze, grenze)
ax.set_xlabel('x [m]', fontsize=14)
ax.set_ylabel('y [m]', fontsize=14)
ax.set_title('Ellipses and street with normals at contact points', fontsize=16)
ax.grid(True)

Ellipses and street with normals at contact points

Equations of Motion¶

# Bodies
Izz_e = 1 / 4 * m_e * (a**2 + b**2)
inertia_e0 = me.inertia(A0, 0, 0, Izz_e)
inertia_e1 = me.inertia(A1, 0, 0, Izz_e)
ellipse0 = me.RigidBody('ellipse0', Dmc0, A0, m_e, (inertia_e0, Dmc0))
ellipse1 = me.RigidBody('ellipse1', Dmc1, A1, m_e, (inertia_e1, Dmc1))
observer0 = me.Particle('observer0', Po0, m_o)
observer1 = me.Particle('observer1', Po1, m_o)
bodies = [ellipse0, ellipse1, observer0, observer1]

# Forces
forces = []
# Gravity
forces.append((Dmc0, -m_e * g * N.y))
forces.append((Dmc1, -m_e * g * N.y))
forces.append((Po0, -m_o * g * N.y))
forces.append((Po1, -m_o * g * N.y))

# Ellipse0 on ellipse1 due to spring
forces.append((CPee1, force_ee(angle_ee0, pen_ee)[0] * N.x +
               force_ee(angle_ee0, pen_ee)[1] * N.y))
forces.append((CPee0, -force_ee(angle_ee0, pen_ee)[0] * N.x -
               force_ee(angle_ee0, pen_ee)[1] * N.y))

# ellipse0 on ellipse1 due to friction
forces.append((CPee1, force_ee_friction(angle_ee0, angle_ee1, pen_ee)[0] *
               N.x + force_ee_friction(angle_ee0, angle_ee1, pen_ee)[1] * N.y))
forces.append((CPee0, -force_ee_friction(angle_ee0, angle_ee1, pen_ee)[0] *
               N.x - force_ee_friction(angle_ee0, angle_ee1, pen_ee)[1] * N.y))

# Street on Ellipse0
forces.append((CPes0, force_es0(X0, pen_se0)[0] * N.x +
               force_es0(X0, pen_se0)[1] * N.y))
# Street on Ellipse1
forces.append((CPes1, force_es1(X1, pen_se1)[0] * N.x +
               force_es1(X1, pen_se1)[1] * N.y))

# Ellipse0 on street due to friction
forces.append((CPes0, force_es0_friction(X0, angle_street0, pen_se0)[0] * N.x +
               force_es0_friction(X0, angle_street0, pen_se0)[1] * N.y))
# Ellipse1 on street due to friction
forces.append((CPes1, force_es1_friction(X1, angle_street1, pen_se1)[0] * N.x +
               force_es1_friction(X1, angle_street1, pen_se1)[1] * N.y))


kd = sm.Matrix([u0 - q0.diff(t), u1 - q1.diff(t),
                ux0 - x0.diff(t), ux1 - x1.diff(t),
                uy0 - y0.diff(t), uy1 - y1.diff(t)])

q_ind = [q0, q1, x0, x1, y0, y1]
u_ind = [u0, u1, ux0, ux1, uy0, uy1]

kanes = me.KanesMethod(N, q_ind, u_ind, kd_eqs=kd)
fr, frstar = kanes.kanes_equations(bodies, forces)
MM = kanes.mass_matrix_full
forcing = kanes.forcing_full
print(f'MM contains {sm.count_ops(MM)} operations')
print(f'forcing contains {sm.count_ops(forcing):,} operations')

qL = [q0, q1, x0, x1, y0, y1, u0, u1, ux0, ux1, uy0, uy1]
pL = [[m_e, m_o, g, a, b, k_spring, amplitude, frequenz, mu],
      [angle_ee0, angle_ee1],
      [X0, X1],
      [angle_street0, angle_street1],
      [pen_ee, pen_se0, pen_se1]
      ]
MM_lam = sm.lambdify(qL + pL, MM, cse=True)
force_lam = sm.lambdify(qL + pL, forcing, cse=True)

MM contains 112 operations
forcing contains 13,118 operations

Numerical Integration¶

grenze = 10.0
accuracy = 50
# brute force search space for minimum distance between ellipse and street
search_space = list(itt.product(np.linspace(-grenze, grenze, accuracy),
                                np.linspace(0, 2*np.pi, accuracy)))

# Use the results from the initial conditions above
angle_ee00 = angle_root_0
angle_ee11 = angle_root_1
X01 = ellipse_street_root[0][0]
X11 = ellipse_street_root[1][0]
angle_street00 = ellipse_street_root[0][1]
angle_street11 = ellipse_street_root[1][1]
pen_ee0 = pen_ee_lam(*([angle_ee00, angle_ee11] + y00 + pL_vals))
pen_se00 = pen_es_lam0(*[X01, angle_street00] + y00 + pL_vals)
pen_se11 = pen_es_lam1(*[X11, angle_street11] + y00 + pL_vals)

pL_vals1 = [pL_vals,
            [angle_ee00, angle_ee11],
            [X01, X11],
            [angle_street00, angle_street11],
            [pen_ee0, pen_se00, pen_se11]
            ]

args_list = []
zeit_list = []


@profile
def gradient(t, y, args):
    # The distances between the ellipses depend continuously on the positions.
    # Therefore we can use the previous solution as a starting point
    # for the next minimization, and then use the result for root.

    def distance_minimizer(X00, args):
        angle0, angle1 = X00
        return distance_ee_lam(*([angle0, angle1] + args))

    x000 = [args[1][0], args[1][1]]
    y123 = list(y)
    arguments = y123 + args[0]
    loesung = minimize(distance_minimizer, x000, arguments)
    args[1][0] = loesung.x[0]
    args[1][1] = loesung.x[1]

    def equations_ee(X00, args):
        angle0, angle1 = X00
        return distance_ee_grad_lam(*([angle0, angle1] + args))

    x000 = [args[1][0], args[1][1]]
    arguments = y123 + args[0]
    loesung = root(equations_ee, x000, arguments)
    args[1][0] = loesung.x[0]
    args[1][1] = loesung.x[1]

    # find the angles and positions, where the distance between the ellipses
    # and the street is minimal.
    # As here the minimum distance does NOT depend continuously on the location
    # of the ellipses, we first do a brute force search, then a minimization,
    # and finally a root search to find the exact minimum.
    for i in range(2):
        distance_array = np.array([distance_lam(*([street_point,
                                                   angle_street] + y123 +
                                                  args[0]))[i]
                                   for street_point, angle_street
                                   in search_space])

        min_distance_index = np.argmin(distance_array)
        street_point_brute = np.linspace(
            -grenze, grenze, accuracy)[min_distance_index // accuracy]
        angle_street_brute = np.linspace(
            0, 2*np.pi, accuracy)[min_distance_index % accuracy]
        args[2][i] = street_point_brute
        args[3][i] = angle_street_brute

    for i in range(2):
        # Search by minimizing the distance function.
        def distance_minimizer(X00, args):
            street_point, angle_street = X00
            return distance_lam(*([street_point, angle_street] + args))[i]

        x000 = [args[2][i], args[3][i]]
        arguments = y123 + args[0]
        loesung = minimize(distance_minimizer, x000, arguments)
        args[2][i] = loesung.x[0]
        args[3][i] = loesung.x[1]

    for i in range(2):
        def equations(X00, args):
            street_point, angle_street = X00
            return distance_grad_lam(*([street_point, angle_street] + args))[i]

        x000 = [args[2][i], args[3][i]]
        arguments = y123 + args[0]
        loesung = root(equations, x000, arguments)
        args[2][i], args[3][i] = loesung.x

    # Find the penetration depths
    args[4][0] = pen_ee_lam(args[1][0], args[1][1], *(y123 + args[0]))
    args[4][1] = pen_es_lam0(args[2][0], args[3][0], *(y123 + args[0]))
    args[4][2] = pen_es_lam1(args[2][1], args[3][1], *(y123 + args[0]))

    args_list.append(deepcopy(args))
    zeit_list.append(t)

    sol = np.linalg.solve(MM_lam(*y, *args), force_lam(*y, *args))
    return np.array(sol).T[0]


interval = 10.0
schritte = int(interval * 650)
times = np.linspace(0., interval, schritte)
t_span = (0., interval)
# If this is not set, the integration will miss the (short) times of contact.
max_step = 0.01

start = time.time()
resultat1 = solve_ivp(gradient, t_span, y00, t_eval=times, args=(pL_vals1,),
                      max_step=max_step)
resultat = resultat1.y.T
print('Shape of result: ', resultat.shape)
print(resultat1.message)
print('Number of function evaluations:', resultat1.nfev)
if choose_symjit:
    msg = ' with symjit'
else:
    msg = ' with lambdify'
print(f"It took {time.time() - start:.2f} seconds to solve the equations"
      f" {msg}")
profiler.print_stats()

Shape of result:  (6500, 12)
The solver successfully reached the end of the integration interval.
Number of function evaluations: 6266
It took 516.51 seconds to solve the equations  with symjit
Timer unit: 1e-07 s

Total time: 396.411 s
File: C:\Users\Peter\github_repos\pst-notebooks\gallery\plot_two_ellipses_bouncing.py
Function: gradient at line 1002

Line #      Hits         Time  Per Hit   % Time  Line Contents
==============================================================
                                         @profile
                                         def gradient(t, y, args):
                                             # The distances between the ellipses depend continuously on the positions.
                                             # Therefore we can use the previous solution as a starting point
                                             # for the next minimization, and then use the result for root.
  1007
    6266      59133.0      9.4      0.0      def distance_minimizer(X00, args):
                                                 angle0, angle1 = X00
                                                 return distance_ee_lam(*([angle0, angle1] + args))
  1011
    6266      49374.0      7.9      0.0      x000 = [args[1][0], args[1][1]]
    6266     177263.0     28.3      0.0      y123 = list(y)
    6266      45592.0      7.3      0.0      arguments = y123 + args[0]
    6266  108352568.0  17292.1      2.7      loesung = minimize(distance_minimizer, x000, arguments)
    6266     158451.0     25.3      0.0      args[1][0] = loesung.x[0]
    6266     107339.0     17.1      0.0      args[1][1] = loesung.x[1]
  1018
    6266      37921.0      6.1      0.0      def equations_ee(X00, args):
                                                 angle0, angle1 = X00
                                                 return distance_ee_grad_lam(*([angle0, angle1] + args))
  1022
    6266      49355.0      7.9      0.0      x000 = [args[1][0], args[1][1]]
    6266      43272.0      6.9      0.0      arguments = y123 + args[0]
    6266   12065799.0   1925.6      0.3      loesung = root(equations_ee, x000, arguments)
    6266     130600.0     20.8      0.0      args[1][0] = loesung.x[0]
    6266     110643.0     17.7      0.0      args[1][1] = loesung.x[1]
  1028
                                             # find the angles and positions, where the distance between the ellipses
                                             # and the street is minimal.
                                             # As here the minimum distance does NOT depend continuously on the location
                                             # of the ellipses, we first do a brute force search, then a minimization,
                                             # and finally a root search to find the exact minimum.
   18798     124325.0      6.6      0.0      for i in range(2):
156687596 2748054736.0     17.5     69.3          distance_array = np.array([distance_lam(*([street_point,
62660000  207319785.0      3.3      5.2                                                     angle_street] + y123 +
62660000  224219433.0      3.6      5.7                                                    args[0]))[i]
31330000  125274542.0      4.0      3.2                                     for street_point, angle_street
31355064  115415133.0      3.7      2.9                                     in search_space])
  1040
   12532     992183.0     79.2      0.0          min_distance_index = np.argmin(distance_array)
   37596    3281005.0     87.3      0.1          street_point_brute = np.linspace(
   25064     165713.0      6.6      0.0              -grenze, grenze, accuracy)[min_distance_index // accuracy]
   37596    2629991.0     70.0      0.1          angle_street_brute = np.linspace(
   25064     174729.0      7.0      0.0              0, 2*np.pi, accuracy)[min_distance_index % accuracy]
   12532      82138.0      6.6      0.0          args[2][i] = street_point_brute
   12532      60319.0      4.8      0.0          args[3][i] = angle_street_brute
  1048
   18798     134273.0      7.1      0.0      for i in range(2):
                                                 # Search by minimizing the distance function.
   12532     107479.0      8.6      0.0          def distance_minimizer(X00, args):
                                                     street_point, angle_street = X00
                                                     return distance_lam(*([street_point, angle_street] + args))[i]
  1054
   12532      97215.0      7.8      0.0          x000 = [args[2][i], args[3][i]]
   12532      87734.0      7.0      0.0          arguments = y123 + args[0]
   12532  301124321.0  24028.4      7.6          loesung = minimize(distance_minimizer, x000, arguments)
   12532     328278.0     26.2      0.0          args[2][i] = loesung.x[0]
   12532     217728.0     17.4      0.0          args[3][i] = loesung.x[1]
  1060
   18798     125984.0      6.7      0.0      for i in range(2):
   12532      81913.0      6.5      0.0          def equations(X00, args):
                                                     street_point, angle_street = X00
                                                     return distance_grad_lam(*([street_point, angle_street] + args))[i]
  1065
   12532      91060.0      7.3      0.0          x000 = [args[2][i], args[3][i]]
   12532      83717.0      6.7      0.0          arguments = y123 + args[0]
   12532   74934241.0   5979.4      1.9          loesung = root(equations, x000, arguments)
   12532     325074.0     25.9      0.0          args[2][i], args[3][i] = loesung.x
  1070
                                             # Find the penetration depths
    6266    4336526.0    692.1      0.1      args[4][0] = pen_ee_lam(args[1][0], args[1][1], *(y123 + args[0]))
    6266    3449932.0    550.6      0.1      args[4][1] = pen_es_lam0(args[2][0], args[3][0], *(y123 + args[0]))
    6266    3228177.0    515.2      0.1      args[4][2] = pen_es_lam1(args[2][1], args[3][1], *(y123 + args[0]))
  1075
    6266    9956523.0   1589.0      0.3      args_list.append(deepcopy(args))
    6266      46804.0      7.5      0.0      zeit_list.append(t)
  1078
    6266   16038617.0   2559.6      0.4      sol = np.linalg.solve(MM_lam(*y, *args), force_lam(*y, *args))
    6266     136493.0     21.8      0.0      return np.array(sol).T[0]

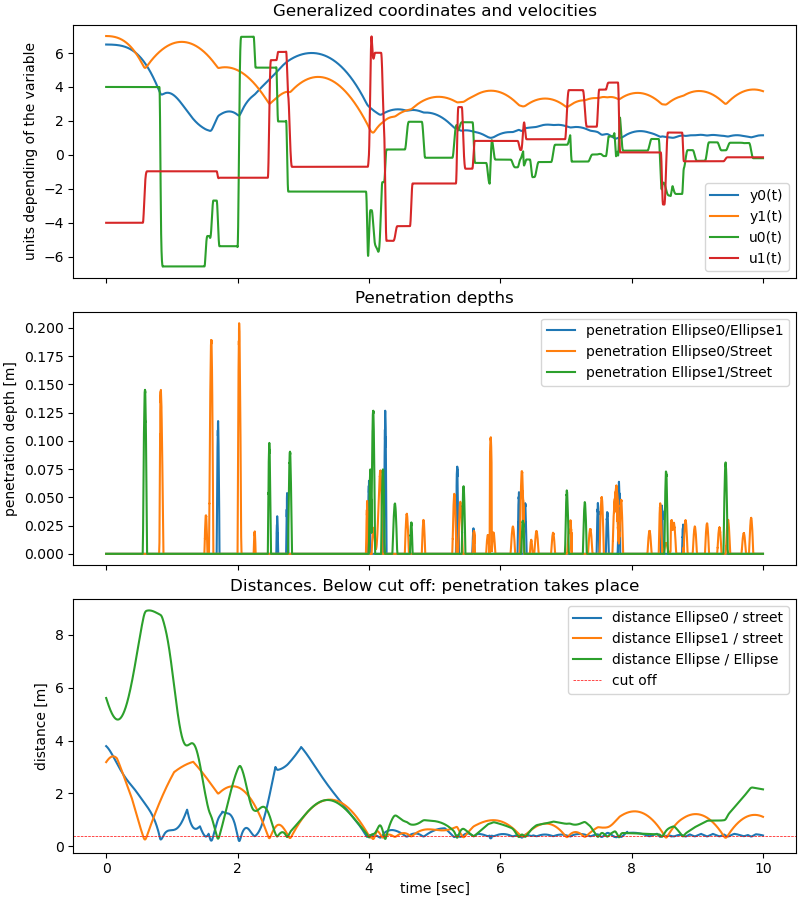
Plot some results

names = [str(i) for i in qL]
fig, ax = plt.subplots(3, 1, figsize=(8, 9), layout='constrained', sharex=True)
for i in (4, 5, 6, 7):
    ax[0].plot(times, resultat[:, i], label=names[i])
    ax[0].set_ylabel('units depending of the variable')
    ax[0].set_title('Generalized coordinates and velocities')
_ = ax[0].legend()


args_1 = [args_list[i][4] for i in range(len(args_list))]
ax[1].plot(zeit_list, [args_1[i][0] for i in range(len(args_1))],
           label='penetration Ellipse0/Ellipse1')
ax[1].plot(zeit_list, [args_1[i][1] for i in range(len(args_1))],
           label='penetration Ellipse0/Street')
ax[1].plot(zeit_list, [args_1[i][2] for i in range(len(args_1))],
           label='penetration Ellipse1/Street')
ax[-1].set_xlabel('time [sec]')
ax[1].set_ylabel('penetration depth [m]')
ax[1].set_title('Penetration depths')
_ = ax[1].legend()

# Find the locations in args_list to match the points returned in resultat.
B = np.array(zeit_list)
A = np.array(resultat1.t)
# Sort B and keep original indices
B_sorted_idx = np.argsort(B)
B_sorted = B[B_sorted_idx]

# Step 2: binary search for closest
pos = np.searchsorted(B_sorted, A)

# Step 3: check neighbors (pos and pos-1) to find which is closer
pos_clipped = np.clip(pos, 1, len(B_sorted)-1)
left = B_sorted[pos_clipped - 1]
right = B_sorted[pos_clipped]
closest_idx_sorted = np.where(
    np.abs(A - left) <= np.abs(A - right),
    pos_clipped - 1,
    pos_clipped
)

# Step 4: convert sorted indices back to original indices of B
closest_idx = B_sorted_idx[closest_idx_sorted]
args_adapted = [args_list[i] for i in closest_idx]

# Plot the distances between the ellipses and the street
# and between the ellipses.
abstand_es_list = []
abstand_ee_list = []
for i in range(len(args_adapted)):
    y00 = list(resultat[i])
    pL_vals = args_adapted[i][0]
    for j in range(2):
        angles = (args_adapted[i][2][j], args_adapted[i][3][j])
        abstand_es_list.append([dist_se0_lam, dist_se1_lam][j](
            *(list(angles) + y00 + pL_vals)))
    angles = (args_adapted[i][1][0], args_adapted[i][1][1])
    abstand_ee_list.append(dist_ee_lam(*(list(angles) + y00 + pL_vals)))

abstand_es_np = np.array(abstand_es_list).reshape((len(resultat1.t), 2))

ax[2].plot(resultat1.t, abstand_es_np[:, 0],
           label='distance Ellipse0 / street')
ax[2].plot(resultat1.t, abstand_es_np[:, 1],
           label='distance Ellipse1 / street')
ax[2].plot(resultat1.t, abstand_ee_list, label='distance Ellipse / Ellipse')
ax[2].axhline(cut_off, color='red', linestyle='--', label='cut off',
              lw=0.5)
ax[2].set_ylabel('distance [m]')
ax[2].set_title('Distances. Below cut off: penetration takes place')
_ = ax[2].legend()

Generalized coordinates and velocities, Penetration depths, Distances. Below cut off: penetration takes place

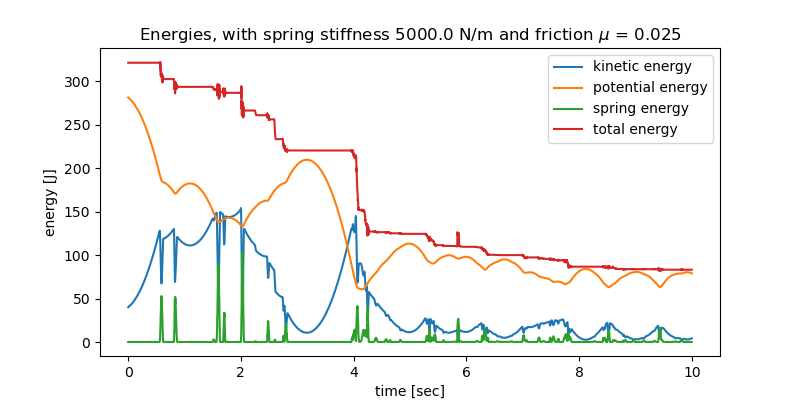
Energy. If mu > 0, it should drop.

kin_energy = sum([koerper.kinetic_energy(N) for koerper in bodies])
pot_energie1 = sum([m_e*g*me.dot(koerper.pos_from(O), N.y)
                   for koerper in (Dmc0, Dmc1)])
pot_energie2 = sum([m_o*g*me.dot(koerper.pos_from(O), N.y)
                   for koerper in (Po0, Po1)])
pot_energie = pot_energie1 + pot_energie2
spring_energie = 0.5 * k_spring * (pen_ee**2 + pen_se0**2 + pen_se1**2)

kin_lam = sm.lambdify(qL + pL, kin_energy, cse=True)
pot_lam = sm.lambdify(qL + pL, pot_energie, cse=True)
spring_lam = sm.lambdify(qL + pL, spring_energie, cse=True)

kin_np = np.empty(len(resultat1.t))
pot_np = np.empty(len(resultat1.t))
spring_np = np.empty(len(resultat1.t))
total_np = np.empty(len(resultat1.t))
for i in range(len(resultat1.t)):
    y00 = list(resultat[i])
    pL_vals = args_adapted
    kin_np[i] = kin_lam(*(y00 + args_adapted[i]))
    pot_np[i] = pot_lam(*(y00 + args_adapted[i]))
    spring_np[i] = spring_lam(*(y00 + args_adapted[i]))
    total_np[i] = kin_np[i] + pot_np[i] + spring_np[i]

fig, ax = plt.subplots(figsize=(8, 4))
ax.plot(resultat1.t, kin_np, label='kinetic energy')
ax.plot(resultat1.t, pot_np, label='potential energy')
ax.plot(resultat1.t, spring_np, label='spring energy')
ax.plot(resultat1.t, total_np, label='total energy')
ax.set_xlabel('time [sec]')
ax.set_ylabel('energy [J]')
msg = r'$\mu$'
ax.set_title(f'Energies, with spring stiffness {k_spring1} N/m '
             f'and friction {msg} = {mu1}')
_ = ax.legend()

$Energies, with spring stiffness 5000.0 N/m and friction $\mu$ = 0.025$

Animation¶

Spit up args_adapted into separate lists for each argument, so CubicSpline can be used

ars_0 = []
args_1 = []
args_2 = []
args_3 = []
args_4 = []
t_arr = np.linspace(0.0, interval, schritte)
for entry in args_adapted:
    ars_0.append(entry[0])
    args_1.append(entry[1])
    args_2.append(entry[2])
    args_3.append(entry[3])
    args_4.append(entry[4])
args_0_sol = CubicSpline(t_arr, ars_0)
args_1_sol = CubicSpline(t_arr, args_1)
args_2_sol = CubicSpline(t_arr, args_2)
args_3_sol = CubicSpline(t_arr, args_3)
args_4_sol = CubicSpline(t_arr, args_4)

fps = 10.0

state_sol = CubicSpline(t_arr, resultat)

coordinates = Dmc0.pos_from(O).to_matrix(N)
for point in (Dmc1, Po0, Po1, CPee0, CPee1, CPes0, CPes1, CPse0, CPse1):
    coordinates = coordinates.row_join(point.pos_from(O).to_matrix(N))

alle = (qL + pL)
coords_lam = sm.lambdify(alle, coordinates, cse=True)


fig, ax = plt.subplots(figsize=(7, 7))
xmin = (np.min(np.concatenate((resultat[:, 2], resultat[:, 3]))) -
        max(a1, b1) - cut_off)
xmax = (np.max(np.concatenate((resultat[:, 2], resultat[:, 3]))) +
        max(a1, b1) + cut_off)
ymax = (np.max(np.concatenate((resultat[:, 4], resultat[:, 5]))) +
        max(a1, b1) + cut_off)
ax.set_xlim(xmin, xmax)

ax.set_aspect('equal')
ax.set_xlabel('x', fontsize=15)
ax.set_ylabel('y', fontsize=15)
ax.axhline(0, color='black', lw=0.5)
ax.axvline(0, color='black', lw=0.5)

# Plot the street
# values for the street
x_street = np.linspace(xmin, xmax, 500)
y_street = street_lam(x_street, amplitude1, frequenz1) + cut_off
ax.plot(x_street, y_street, color='black', linestyle='-', linewidth=1)

ymin = np.min(y_street) - 1.0
ax.set_ylim(ymin, ymax)

t = 0.0
coords = coords_lam(*state_sol(t), args_0_sol(t), args_1_sol(t),
                    args_2_sol(t), args_3_sol(t), args_4_sol(t))

# draw the ellipses, their mass centers, the observers
ellipse0 = Ellipse((coords[0, 0], coords[1, 0]), width=2*a1 + cut_off,
                   height=2*b1 + cut_off, angle=np.rad2deg(y00[0]),
                   facecolor='red', edgecolor='black', label=f'ellipse 0',
                   alpha=0.5)
ax.add_patch(ellipse0)

ellipse1 = Ellipse((coords[0, 1], coords[1, 1]), width=2*a1 + cut_off,
                   height=2*b1 + cut_off, angle=np.rad2deg(y00[1]),
                   edgecolor='black', facecolor='blue', alpha=0.5,
                   label=f'ellipse 1')
ax.add_patch(ellipse1)

# centers of the ellipses
point_Dmc0 = ax.scatter([coords[0, 0]], [coords[1, 0]], color='red',
                        edgecolors='black', s=20)
point_Dmc1 = ax.scatter([coords[0, 1]], [coords[1, 1]], color='blue',
                        edgecolors='black', s=20)
# particles on the ellipses
point_Po0 = ax.scatter([coords[0, 2]], [coords[1, 2]], color='yellow', s=30,
                       edgecolors='black')
point_Po1 = ax.scatter([coords[0, 3]], [coords[1, 3]], color='yellow', s=30,
                       edgecolors='black')

# Points of closest distance between the ellipses and the street
point_CPee0 = ax.scatter([coords[0, 4]], [coords[1, 4]], color='black', s=30)
point_CPee1 = ax.scatter([coords[0, 5]], [coords[1, 5]], color='black', s=30)
point_CPes0 = ax.scatter([coords[0, 6]], [coords[1, 6]], color='black', s=30)
point_CPes1 = ax.scatter([coords[0, 7]], [coords[1, 7]], color='black', s=30)
point_CPse0 = ax.scatter([coords[0, 8]], [coords[1, 8]], color='black', s=30)
point_CPse1 = ax.scatter([coords[0, 9]], [coords[1, 9]], color='black', s=30)

line_ee, = ax.plot([coords[0, 4], coords[0, 5]], [coords[1, 4], coords[1, 5]],
                   color='green', linestyle='-', linewidth=0.5)
line_e0s, = ax.plot(
    [coords[0, 6], coords[0, 8]], [coords[1, 6], coords[1, 8]], color='red',
    linestyle='-', linewidth=0.5)
line_e1s, = ax.plot(
    [coords[0, 7], coords[0, 9]], [coords[1, 7], coords[1, 9]], color='blue',
    linestyle='-', linewidth=0.5)

# Function to update the plot for each animation frame


def update(t):
    message = (f'Running time {t:.2f} sec \n The yellow dots are observers. \n'
               f'The lines indicate the minimal distances.')
    ax.set_title(message, fontsize=12)

    coords = coords_lam(*state_sol(t), args_0_sol(t), args_1_sol(t),
                        args_2_sol(t), args_3_sol(t), args_4_sol(t))
    point_Dmc0.set_offsets([coords[0, 0], coords[1, 0]])
    point_Dmc1.set_offsets([coords[0, 1], coords[1, 1]])
    point_Po0.set_offsets([coords[0, 2], coords[1, 2]])
    point_Po1.set_offsets([coords[0, 3], coords[1, 3]])
    point_CPee0.set_offsets([coords[0, 4], coords[1, 4]])
    point_CPee1.set_offsets([coords[0, 5], coords[1, 5]])
    point_CPes0.set_offsets([coords[0, 6], coords[1, 6]])
    point_CPes1.set_offsets([coords[0, 7], coords[1, 7]])
    point_CPse0.set_offsets([coords[0, 8], coords[1, 8]])
    point_CPse1.set_offsets([coords[0, 9], coords[1, 9]])

    ellipse0.set_center((coords[0, 0], coords[1, 0]))
    ellipse0.angle = np.rad2deg(state_sol(t)[0])

    ellipse1.set_center((coords[0, 1], coords[1, 1]))
    ellipse1.angle = np.rad2deg(state_sol(t)[1])

    line_ee.set_data(
        [coords[0, 4], coords[0, 5]], [coords[1, 4], coords[1, 5]])
    line_e0s.set_data(
        [coords[0, 6], coords[0, 8]], [coords[1, 6], coords[1, 8]])
    line_e1s.set_data(
        [coords[0, 7], coords[0, 9]], [coords[1, 7], coords[1, 9]])


# Create the animation
animation = FuncAnimation(
    fig, update, frames=np.arange(0.0, interval, 1 / fps),
    interval=1000 / fps, blit=False)
plt.show()

Total running time of the script: (9 minutes 18.352 seconds)

Gallery generated by Sphinx-Gallery

Two Ellipses Bouncing on a Wavy Street¶

Objectives¶

Description¶

Finding the points of least distance¶

Notes¶

Equations of Motion¶

Numerical Integration¶

Animation¶

Peter's Mechanics Examples

Navigation

Related Topics