Note
Go to the end to download the full example code.
Automatic Balancing of a Wheel¶
Objective¶
Show how to simulate the automatic balancing of a wheel with free particles as shown in this video: https://www.youtube.com/watch?v=T47s4L1Wje4
Description¶
A disc of radius \(\textrm{radius}\) is rotating with a constant angular velocity \(\omega\) around the vertical axis in the horizontal X / Y plane.
It’s center is tied to the origin by a spring with a spring constant \(k\) and a damping coefficient \(\textrm{speed}_{\mu}\). The disc has a fixed imbalance created by a particle of mass \(m_i\) at a distance of \(\textrm{radius}\) from the center of the disc.
A number n_free of particles of mass \(m_f\) are free to move on the
perimeter of the disc.
Notes¶
Without adding friction to the attachment of the disc to the origin and to the motion of the free particles, it did not work.
With one or two free particles there is only one solution, but with three there are two solutions. One is found.
States
\(x, y\) : coordinates of the center of the disc in the inertial frame
\(u_x, u_y\) : velocities of the center of the disc in the inertial frame
\(q_i\) : angular coordinates of the free particles relative to the disc
\(u_i\) : angular velocities of the free particles relative to the disc
Parameters
\(m_{\textrm{disc}}\) : mass of the disc
\(m_i\) : mass of the fixed particle
\(m_f\) : mass of the free particles
\(g\) : gravity
\(\textrm{speed}_{\mu}\) : damping coefficient for the disc
\(\textrm{free}_{\mu}\) : damping coefficient for the free particles
\(\omega\) : angular velocity of the disc
\(k\) : spring constant of the spring connecting the disc to the origin
\(\textrm{radius}\) : radius of the disc
import sympy as sm
import sympy.physics.mechanics as me
import numpy as np
from scipy.integrate import solve_ivp
from scipy.interpolate import CubicSpline
from matplotlib.patches import Circle
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
Equations of Motion, Kanes Method¶
n_free = 2 # number of free particles
N, A = sm.symbols('N A', cls=me.ReferenceFrame)
O, O_disc, Po = sm.symbols('O, O_disc, Po', cls=me.Point)
Points = sm.symbols(f'P:{n_free}', cls=me.Point)
t = me.dynamicsymbols._t
O.set_vel(N, 0)
# Coordinates and velocities of the center of the disc, w.r.t. N
x, y, ux, uy = me.dynamicsymbols('x, y, ux, uy')
# Coordinates and velocities of the free particles, w.r.t. the disc
q = me.dynamicsymbols(f'q:{n_free}')
u = me.dynamicsymbols(f'u:{n_free}')
m_disc, m_i, m_f, g, speed_mu, free_mu, omega, k, radius = sm.symbols(
'm_disc, m_i, m_f, g, speed_mu, free_mu, omega, k, radius', real=True)
A.orient_axis(N, omega * t, N.z)
A.set_ang_vel(N, omega * N.z)
# Center of the disc
O_disc.set_pos(O, x * N.x + y * N.y)
O_disc.set_vel(N, ux * N.x + uy * N.y)
# Fixed imbalance
Po.set_pos(O_disc, radius/sm.sqrt(2) * (A.x + A.y))
# Free particles
vel_x = []
vel_y = []
for i in range(n_free):
Points[i].set_pos(O_disc, radius * (sm.cos(q[i]) * A.x + radius *
sm.sin(q[i]) * A.y))
# Needed for the dampening of the free particles.
v_A = Points[i].pos_from(O_disc).diff(t, A)
vel_x.append(v_A.dot(A.x))
vel_y.append(v_A.dot(A.y))
Define the bodies.
bodies = []
iZZ = 0.5 * m_disc * radius**2
inertia = me.inertia(A, 0, 0, iZZ)
disc = me.RigidBody('disc', O_disc, A, m_disc, (inertia, O_disc))
bodies.append(disc)
P_fix = me.Particle('P_fix', Po, m_i)
bodies.append(P_fix) # fixed particle
for i in range(n_free):
bodies.append(me.Particle(f'P_{i}', Points[i], m_f))
Define the forces.
vektor = O_disc.pos_from(O)
indikator = sm.Piecewise((0, vektor.magnitude() < 1.e-16), (1, True))
forces = [(O_disc, -k * indikator * vektor - speed_mu * (ux * N.x + uy * N.y))]
indikator = sm.Piecewise((0, omega < 1.e-16), (1, True))
for i in range(n_free):
vektor = Points[i].pos_from(O_disc)
speed = vektor.cross(indikator * N.z)
forces.append((Points[i], - free_mu * (vel_x[i] * A.x + vel_y[i] * A.y)))
# Kinematic equations
kd = [ux - x.diff(t), uy - y.diff(t), *[u[i] - q[i].diff(t)
for i in range(n_free)]]
q_ind = [x, y, *q]
u_ind = [ux, uy, *u]
KM = me.KanesMethod(N, q_ind, u_ind, kd)
fr, frstar = KM.kanes_equations(bodies, forces)
MM = KM.mass_matrix_full
force = KM.forcing_full
print('force dynamic symbols', me.find_dynamicsymbols(force))
print('mass matrix dynamic symbols', me.find_dynamicsymbols(MM))
print(f'force contains {sm.count_ops(force)} operations')
print(f'mass matrix contains {sm.count_ops(MM)} operations')
force dynamic symbols {u0(t), u1(t), ux(t), q1(t), uy(t), x(t), q0(t), y(t)}
mass matrix dynamic symbols {q1(t), q0(t)}
force contains 596 operations
mass matrix contains 154 operations
Lambdification
qL = q_ind + u_ind
pL = [m_disc, m_i, m_f, g, speed_mu, free_mu, omega, k, radius, t]
MM_lam = sm.lambdify(qL + pL, MM, cse=True)
force_lam = sm.lambdify(qL + pL, force, cse=True)
Numerical Integration¶
# Input variables
m_disc1 = 20.0 # mass of the disc
m_i1 = 1.0 # mass of the fixed particle
m_f1 = 1.0 # mass of the free particles
g1 = 9.81 # gravity
radius1 = 1.0 # radius of the disc
speed_mu1 = 1.0 # damping coefficient for the disc
free_mu1 = 0.5 # friction coefficient for the free particles
k1 = 1.e1 # spring constant
omega1 = 1.5 # angular velocity of the disc
x1 = 0.0 # initial x position of the disc
y1 = 0.0 # initial y position of the disc
ux1 = 0.0 # initial x velocity of the disc
uy1 = 0.0 # initial y velocity of the disc
q01 = np.deg2rad(55)
q11 = np.deg2rad(15)
q21 = np.deg2rad(0.0) # initial angle of the first free particle
u01 = 0.0
u11 = 0.0
u21 = 0.0
t1 = 0.0
intervall = 100
punkte = 100
schritte = int(intervall * punkte)
times = np.linspace(0., intervall, schritte)
t_span = (0., intervall)
pL_vals = [m_disc1, m_i1, m_f1, g1, speed_mu1, free_mu1, omega1, k1,
radius1, t1]
if n_free == 1:
y0 = [x1, y1, q01, ux1, uy1, u01]
elif n_free == 2:
y0 = [x1, y1, q01, q11, ux1, uy1, u01, u11]
elif n_free == 3:
y0 = [x1, y1, q01, q11, q21, ux1, uy1, u01, u11, u21]
else:
raise ValueError(f'Unsupported number of free particles: {n_free}',
'Set manually in the code above')
def gradient(t, y, args):
args[-1] = t # Update time in args
sol = np.linalg.solve(MM_lam(*y, *args), force_lam(*y, *args))
return np.array(sol).T[0]
resultat1 = solve_ivp(gradient, t_span, y0, t_eval=times, args=(pL_vals,),
method='Radau', atol=1.e-10, rtol=1.e-10)
resultat = resultat1.y.T
print('resultat shape', resultat.shape, '\n')
print(resultat1.message)
resultat shape (10000, 8)
The solver successfully reached the end of the integration interval.
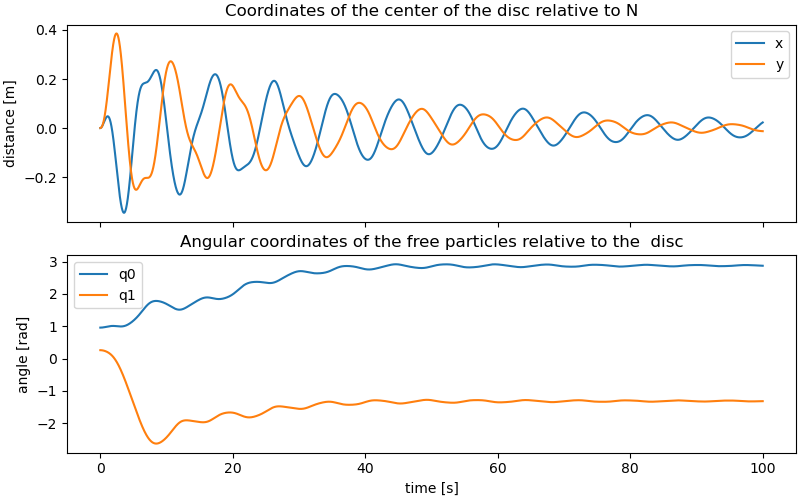
Plot some results.
fig, ax = plt.subplots(2, 1, figsize=(8, 5), layout='constrained',
sharex=True)
bezeichnung = ['x', 'y', 'q0', 'q1', 'ux', 'uy', 'u0', 'u1']
for i in range(2):
ax[0].plot(times, resultat[:, i], label=bezeichnung[i])
ax[0].legend()
ax[0].set_ylabel('distance [m]')
ax[0].set_title('Coordinates of the center of the disc relative to N')
for i in range(2, 2 + n_free):
ax[1].plot(times, resultat[:, i], label=bezeichnung[i])
ax[1].set_xlabel('time [s]')
ax[1].set_ylabel('angle [rad]')
ax[1].set_title('Angular coordinates of the free particles relative to the '
' disc')
_ = ax[1].legend()
Animation¶
fps = 10.0
t_arr = np.linspace(0.0, intervall, schritte)
state_sol = CubicSpline(t_arr, resultat)
r_disc = radius1
Pl, Pr, Pu, Pd = sm.symbols('Pl Pr Pu Pd', cls=me.Point)
Pl.set_pos(O_disc, -r_disc*A.x)
Pr.set_pos(O_disc, r_disc*A.x)
Pu.set_pos(O_disc, r_disc*A.y)
Pd.set_pos(O_disc, -r_disc*A.y)
coordinates = O_disc.pos_from(O).to_matrix(N)
for point in (Po, Pl, Pr, Pu, Pd, *Points):
coordinates = coordinates.row_join(point.pos_from(O).to_matrix(N))
coords_lam = sm.lambdify(qL + pL, coordinates, cse=True)
fig, ax = plt.subplots(figsize=(7, 7))
ax.set_xlim(-r_disc-1, r_disc+1)
ax.set_ylim(-r_disc-1, r_disc+1)
ax.set_aspect('equal')
ax.set_xlabel('x', fontsize=15)
ax.set_ylabel('y', fontsize=15)
ax.axhline(0, color='black', lw=0.5)
ax.axvline(0, color='black', lw=0.5)
# draw the spokes
line1, = ax.plot([], [], lw=1, marker='o', markersize=0, color='black')
line2, = ax.plot([], [], lw=1, marker='o', markersize=0, color='black')
# draw the ball
initial_center = (x1, y1)
ball = Circle(initial_center, r_disc,
fill=True, color='magenta', alpha=0.5)
ax.add_patch(ball)
# draw the observer
imbalance, = ax.plot([], [], marker='o', markersize=15, color='black')
# The free balls
free_balls = []
farben = ['red', 'yellow', 'blue'] # Colors for the free balls
for i in range(n_free):
free_balls.append(ax.plot([], [], marker='o', markersize=15,
color=farben[i])[0])
# Function to update the plot for each animation frame
def update(t):
message = ((f'Running time {t:.2f} sec \n The black particle is the '
f'imbalance. \n The colored particles are free to move to '
'balance the wheel.'))
ax.set_title(message, fontsize=12)
pL_vals[-1] = t # Update time in pL_vals
coords = coords_lam(*state_sol(t), *pL_vals)
line1.set_data([coords[0, 2], coords[0, 3]], [coords[1, 2], coords[1, 3]])
line2.set_data([coords[0, 4], coords[0, 5]], [coords[1, 4], coords[1, 5]])
imbalance.set_data([coords[0, 1]], [coords[1, 1]])
ball.set_center((coords[0, 0], coords[1, 0]))
for i in range(n_free):
free_balls[i].set_data([coords[0, 6 + i]], [coords[1, 6 + i]])
# Create the animation
animation = FuncAnimation(fig, update, frames=np.arange(0.0,
intervall, 1 / fps),
interval=400/fps, blit=False)
plt.show()