Note
Go to the end to download the full example code.
Spoked, Rimless Wheel¶
Objectives¶
Show how to use the event feature of solve_ivp, which allows to stop the integration when an event has occured, here a second spoke hits the road.
Show how to use Kane’s equations of motion to set up the equations of motion for a more difficult problem.
Introduction¶
A wheel with n spokes distributed evenly around the hub \(Dmc\) with mass \(m_{Dmc}\), having lengths \(l_0...l_{n-1}\), with spoke \(sp_i\) havimg mass \(m_{sp_i}\), center of mass \(Dmc_{sp_i}\) and moment of inertia around the Z - axis of \(iZZ_{sp_i}\), and having a particle \(DmcE_{sp_i}\) at the end is ‘rolling’ on an uneven street. It is described here: http://ruina.tam.cornell.edu/research/topics/locomotion_and_robotics/tinkertoy_walker/prediction_stable_walking_error_analysis.pdf
Notes¶
Not all eventualities are considered. If, for example, the street is shaped in such a way that a portion of the spoke will touch it before its end point does, this is ignored.
There is the option to make it ‘look like an ellipse’ by giving the spokes the appropriate lengths.
It may be noteworthy, that the rotational speed of the wheel may change discontinuously, when a new spoke touches the street. This is because the moment of inertia changes, and the total energy must be conserved.
import sympy as sm
import sympy.physics.mechanics as me
import numpy as np
from scipy.integrate import solve_ivp
from scipy.optimize import fsolve
from matplotlib import animation
import matplotlib as mp
import matplotlib.pyplot as plt
Set the geometry, define points, etc.
For each spoke touching the ground, a separate Kane’s EOMs is set up fuerther down. This requires, that different points for each EOM are defined, while of course, they physically describe the same object, e.g. the center of the wheel.
n = 7 # number of spokes
#=============================
if isinstance(n, int) is False or n <= 2:
raise Exception('n must be an integer larger than 2')
N = me.ReferenceFrame('N')
O = me.Point('O')
O.set_vel(N, 0)
t = me.dynamicsymbols._t
Dmc = list(sm.symbols(f'Dmc {0}:{n}', cls=me.Point)) # mass center of the wheel
# body fixed frames of each spoke
A = list(sm.symbols(f'A{0}:{n}', cls=me.ReferenceFrame))
# length of each spoke
l = list(sm.symbols(f'l{0}:{n}'))
DmcEsp = [[sm.symbols('DmcEsp' + str(i) + str(j), cls=me.Point)
for j in range(n)] for i in range(n)] # end points of each spoke
Dmcsp = [[sm.symbols('Dmcsp' + str(i) + str(j), cls=me.Point)
for j in range(n)] for i in range(n)] # mass centers of each spoke
CP = sm.symbols(f'CP', cls=me.Point) # contact points of each spoke with the street
# x - coordinate of the contact point of the wheel with the street, of course
# y - coordinate is: gesamt(x0, amamplitude, frequenz)
x0 = sm.symbols(f'x0')
mDmc = sm.symbols('mDmc') # mass of center of the wheel
msp = list(sm.symbols(f'msp{0}:{n}')) # mass of each spoke
mEsp = list(sm.symbols(f'mEsp{0}:{n}')) # mass of each end point of each spoke
spoke_no = sm.symbols('spoke_no', int=True)
amplitude, frequenz = sm.symbols('amplitude, frequenz') # for the road profile
reibung, g = sm.symbols('reibung, g') # friction coefficient 'in the' wheel,
# gravity
q, u = me.dynamicsymbols('q, u') # generalized coordinates and speeds of the
# wheel
phi = 2 * sm.pi / n # angle between each spoke
A[0].orient_axis(N, q, N.z) # orientation of the wheel
A[0].set_ang_vel(N, u * N.z) # angular velocity of the wheel
for i in range(1, n): # orientation of each spoke
A[i].orient_axis(A[0], i * phi, N.z)
Modeling the street
rumpel = 3 # the higher the number the more 'uneven the street'
#==============================================================
def gesamt(x, amplitude, frequenz):
strasse = sum([amplitude/j * sm.sin(j*frequenz * x)
for j in range(1, rumpel)])
strassen_form = (frequenz/4. * x)**2
return strassen_form + strasse
Set up Kanes Equations¶
value is the number of the spoke presently touching the street
Dmc_ort_list = []
DmcEsp_ort_list = []
Dmcsp_ort_list = []
BODY_list = []
def KANE(value, drucken=False):
# set up Kane's equations for each spoke
# contact point of the spoke touching the street with the street
CP.set_pos(O, x0*N.x + gesamt(x0, amplitude, frequenz)*N.y)
CP.set_vel(N, 0)
# endpoint of spoke nummber 'value' is contacting the street
DmcEsp[value][value].set_pos(CP, 0)
DmcEsp[value][value].set_vel(N, 0)
Dmc[value].set_pos(DmcEsp[value][value], -l[value]*A[value].x)
Dmc[value].v2pt_theory(DmcEsp[value][value], N, A[value])
Dmcsp[value][value].set_pos(DmcEsp[value][value], -l[value]/2.*A[value].x)
Dmcsp[value][value].v2pt_theory(DmcEsp[value][value], N, A[value])
for i in range(n):
Dmcsp[value][i].set_pos(Dmc[value], l[i]/2. * A[i].x)
Dmcsp[value][i].v2pt_theory(Dmc[value], N, A[i])
DmcEsp[value][i].set_pos(Dmc[value], l[i] * A[i].x)
DmcEsp[value][i].v2pt_theory(Dmc[value], N, A[i])
Dmc_ort_list.append(Dmc[value].pos_from(O))
DmcEsp_ort_list.append([DmcEsp[value][i].pos_from(O) for i in range(n)])
Dmcsp_ort_list.append([Dmcsp[value][i].pos_from(O) for i in range(n)])
BODY = [me.Particle('pDmc', Dmc[value], mDmc)]
for i in range(n):
BODY.append(me.Particle(f'pDmcEsp{value}{i}', DmcEsp[value][i],
mEsp[i]))
iZZ = 1./12. * msp[i] * l[i]**2
I = me.inertia(A[i], 0, 0, iZZ)
BODY.append(me.RigidBody(f'spoke{value}{i}', Dmcsp[value][i],
A[i], msp[i], (I, Dmcsp[value][i])))
BODY_list.append(BODY)
FL = [(Dmc[value], -mDmc * g * N.y)]
for i in range(n):
FL.append((Dmcsp[value][i], -msp[i] * g * N.y))
FL.append((DmcEsp[value][i], -mEsp[i] * g * N.y))
FL.append((A[0], -u * reibung * N.z)) # 'internal' damping of the wheel
kd = [u - q.diff()]
q_ind = [q]
u_ind = [u]
KM = me.KanesMethod(N, q_ind, u_ind, kd_eqs=kd)
fr, frstar = KM.kanes_equations(BODY, FL)
MM = KM.mass_matrix_full
force = KM.forcing_full
if drucken == True:
print('MM DS', me.find_dynamicsymbols(MM))
print('MM FS', MM.free_symbols)
print(f'MM has {sm.count_ops(MM)} operations, '
f'{sm.count_ops(sm.count_ops(sm.cse(MM)))} after cse, \n')
print('force DS', me.find_dynamicsymbols(force))
print('force FS', force.free_symbols)
print(f'force has {sm.count_ops(force)} operations, '
f'{sm.count_ops(sm.count_ops(sm.cse(force)))} after cse, \n')
return [MM, force]
Kane’s equations of motion for each spoke.
# Drucken = True: print some statistics of each mass matrix and each
# forcing vector.
drucken = False
MM_list = ['m' + str(j) for j in range(n)]
force_list = ['f' + str(j) for j in range(n)]
for i in range(n):
MM, force = KANE(i, drucken)[0:2]
MM_list[i] = MM
force_list[i] = force
Set up various functions needed laterFor each spoke_no, the ‘name’ of the spoke touching the street, a separate energy is needed.
kin_energie = [sum(body.kinetic_energy(N) for body in BODY_list[i])
for i in range(n)]
pot_energie = []
for value in range(n):
pot_energie1 = 0
pot_energie1 += mDmc * g * Dmc[value].pos_from(O).dot(N.y)
pot_energie1 += sum([m * g * body.pos_from(O).dot(N.y) for m, body in
zip(mEsp, DmcEsp[value])])
pot_energie1 += sum([m * g * body.pos_from(O).dot(N.y) for m, body in
zip(msp, Dmcsp[value])])
pot_energie.append(pot_energie1)
gesamt1 = gesamt(x0, amplitude, frequenz)
# these are the locations of the points, needed for the animation
Dmc_loc = []
DmcEsp_loc = []
Dmcsp_loc = []
for i in range(n):
Dmc_loc.append([Dmc_ort_list[i].dot(uv) for uv in (N.x, N.y)])
DmcEsp_loc.append([[DmcEsp_ort_list[i][j].dot(uv) for uv in (N.x, N.y)]
for j in range(n)])
Dmcsp_loc.append([[Dmcsp_ort_list[i][j].dot(uv) for uv in (N.x, N.y)]
for j in range(n)])
test = np.array(DmcEsp_loc)
Lambdification
qL = [q, u]
pL = [mDmc] + msp + mEsp + l + [amplitude, frequenz, reibung, g] + [x0, spoke_no]
MM_lam = sm.lambdify(qL + pL, MM_list, cse=True)
force_lam = sm.lambdify(qL + pL, force_list, cse=True)
kin_lam = sm.lambdify(qL + pL, kin_energie, cse=True)
pot_lam = sm.lambdify(qL + pL, pot_energie, cse=True)
gesamt1_lam = sm.lambdify([x0, amplitude, frequenz], gesamt1, cse=True)
Dmc_loc_lam = sm.lambdify(qL + pL, Dmc_loc, cse=True)
DmcEsp_loc_lam = sm.lambdify(qL + pL, DmcEsp_loc, cse=True)
Dmcsp_loc_lam = sm.lambdify(qL + pL, Dmcsp_loc, cse=True)
New angular velocity As the spokes may be of different lengths and masses, the moment of inertia will generally change, when a new spoke touches the street and becomes the new ‘contact point, see here: https://en.wikipedia.org/wiki/Parallel_axis_theorem In order to keep the total energy constant, the angular velocity must change discontinuously, too. (Of course the potential energy cannot change discontinuoulsy, infiniterly strong forces would be reqired for this) The new angular velocity is calculated here.
u_neu = sm.symbols('u_neu')
def new_speed(q_old, u_old, speiche_neu, x0_neu, args):
kin_alt = kin_lam(q_old, u_old, *args)[args[-1]]
kin_neu = kin_energie[speiche_neu]
kin_neu_lam = sm.lambdify([u] + [q] + pL, kin_neu - kin_alt, cse=True)
def func(y, args1):
return kin_neu_lam(y, *args1)
y = u_old
pL_vals1 = [pL_vals[i] for i in range(len(pL_vals)-2)]
args1 = [q_old] + pL_vals1 + [x0_neu, speiche_neu]
ergebnis = fsolve(func, y, args1)
return ergebnis
This function calculates the distance in Y direction of the end point of each spoke from the street.
def abstand(y, args):
'''
this function calculates the distance between the end points of each spoke
and the street it returns: the number of the spoke i, its X coordinate,
and its Y distance from the street
'''
DELTA = []
for i in range(n):
x_coord = DmcEsp_loc_lam(*y, *args)[args[-1]][i][0]
delta1 = (DmcEsp_loc_lam(*y, *args)[args[-1]][i][1] -
gesamt1_lam(x_coord, args[-6], args[-5]))
DELTA.append([i, x_coord, delta1])
return DELTA
This function triggers an event with solve_ivp, if any spoke, other than the one currently touching the street, is close to touching the stree, too.
def event(t, y, args):
global new_x0, new_spoke_no, zaehl_event, delta
zaehl_event += 1
'''
this function checks, whether any of the spokes touches the street.
if a second spoke is about to touch the street, the function returns 1.
If solve_ivp 'decides' that an event has happened, the new X ccordinate
and the 'new' spoke touching the street are available via global.
(I see no other way of doing it, as event is limited as to what it is
allowed to return.)
spoke_no is the number of the spoke which is going to touch the street
next, x0 is the x coordinate of the contact point of the wheel with the
street
'''
DELTA = abstand(y, args)
DELTA1 = min(DELTA, key=lambda x: x[2])
new_spoke_no, new_x0, delta = DELTA1[0], DELTA1[1], DELTA1[2]
if delta >= 1.e-5:
return -1
else:
if new_spoke_no != args[-1]:
return 1.
else:
return -1.
Set the initial conditions and the parameters for the numerical integration
#==============================================================================
ellipse = False # if True, the wheel is drawn as an ellipse, if False,
# whatever you set it at.
#==============================================================================
def ellipse_radius(a, b, phi):
'''
this function calculates the radius of the ellipse at the angle phi,
measured from the x-axis
'''
return a * b / np.sqrt((b * np.cos(phi))**2 + (a * np.sin(phi))**2)
# enter the values of the parameters and initial conditions here
mDmc1 = 1. # mass of the wheel
mEsp1 = [1. + i/2 for i in range(n)] # mass of the end points of each spoke
l1 = [3. - 2*i/n for i in range(n)] # length of each spoke
msp1 = [1. * l1[i] for i in range(n)] # mass of each spoke
if ellipse == True:
a1 = 2. # semi-axis of the wheel
b1 = 1. # semi-axis of the wheel2
phi = 2 * np.pi / n
for i in range(n):
l1[i] = ellipse_radius(a1, b1, i * phi)
msp1[i] = 1./n * l1[i]
# Should be zero, but this will cause numerical problems:
# The mass matrix will be singular
mEsp1[i] = 0.0000001
amplitude1 = 1.
frequenz1 = 0.75
reibung1 = 0.
g1 = 9.81
x01 = 5.
spoke_no1 = 0
q1 = -np.pi/2.
u1 =-5.
intervall = 30.
punkte = 200 # punkte * invervall is the number of points in time
#=======================================================================================================
pL_vals = ([mDmc1] + msp1 + mEsp1 + l1 + [amplitude1, frequenz1, reibung1, g1]
+ [x01, spoke_no1])
y0 = [q1, u1]
# check, that only the spoke labelled spoke_no1 touches the street at the
# beginning
DELTA = abstand(y0, pL_vals)
for i, x_coord, delta in DELTA:
if delta < 1e-5 and i != spoke_no1:
print(f'Spoke {i} touches the street at the beginning, '
f'change l1({spoke_no1}) or change x01, or change q1')
raise Exception()
Numerical integration¶
keyword events in solve_ivp: In this case an event has happened, if a second contact point was found. A function has to be definded (Called it event), such that it returns a negative real value if the even has not happened, and a positive real value if it has happened. https://stackoverflow.com/questions/76233727/scipys-solve-ivp-has-a-keyword-events-my-question-is-regarding-this-keyword?rq=2
If (as done here, of course), event.terminal = True, solve_ivp stops when the event has happened and returns the results obtained so far. They are in ergebnis. Then the new \(\dfrac{d}{dt}q(t)\) for the new inital values, as in general the angular velocity changes discontinuously with a new contact point.
Note: if the result of solve_ivp(…) is called resultat, then resultat.y_events[i][j][k] holds the value of the k-th coordinate (of the result of the integration) when the i-th event has happend for the (j+1)-th time. Since I use event_terminal = True, and there is only one event, i = j = 0 in this example resultat.t_events[i][j] hold the time when the i-th event has happened for the (j+1)-th time.
#==============================================================================
event_info = False # if True, data related to the occurence of events
#are printed
#==============================================================================
schritte = int(intervall * punkte)
times = np.linspace(0, intervall, schritte)
zaehl_event = 0 # number of calls of the event function
sprungzeit = [] # list of the times, when the wheel touches the street
params = [] # collects nw_x0 and new_spoke_no
# store the values of spoke_no and x0, used with the previous integration
old_spoke, old_x0 = pL_vals[-1], pL_vals[-2]
#==============================================
event.terminal = True # if True, this stops the integration if and when event
#occurs
def gradient(t, y, args):
vals = np.concatenate((y, args))
# select the mass matrix and the forcing vector of the spoke which is
# currently touching the street
sol = np.linalg.solve(MM_lam(*vals)[args[-1]], force_lam(*vals)[args[-1]])
return np.array(sol).T[0]
starttime = 0.
ergebnis = [] # partial results of the integration are collected here
event_dict = {-1: 'Integration failed', 0: 'Integration finished successfully',
1: 'some termination event'}
funktionsaufrufe = 0 # number of calls of the rhs of the ode
here the ‘piecewise’ integration starts.
while starttime < intervall:
resultat1 = solve_ivp(gradient, (starttime, float(intervall)), y0,
t_eval=times, args=(pL_vals,), events=event,
atol=1.e-7, rtol=1.e-7, max_step=0.01)
resultat = resultat1.y.T
ergebnis.append(resultat)
funktionsaufrufe += resultat1.nfev
if len(resultat1.y_events[0]) > 0:
if event_info is True:
print((f'new_x0 = {new_x0:.3f}, new_spoke_no = {new_spoke_no}, '
f'time {resultat1.t_events[0][0]:.3f}, '
f' u = {resultat1.y_events[0][0][1]:.3f}, '
f'q = {resultat1.y_events[0][0][0]:.3f}, '
f'distance of spoke to ground = {delta:.3e}, '
f' shape of resultat: {resultat.shape}'))
params.append([resultat.shape[0], old_spoke, old_x0])
new_u = new_speed(resultat1.y_events[0][0][0],
resultat1.y_events[0][0][1], new_spoke_no, new_x0,
pL_vals) # get the new speed of the wheel,
# to keep total energy constant.
pL_vals[-1] = new_spoke_no
pL_vals[-2] = new_x0
y0 = [resultat1.y_events[0][0][0], new_u[0]]
zeit = resultat1.t_events[0][0]
sprungzeit.append(zeit)
old_spoke, old_x0 = new_spoke_no, new_x0
starttime = resultat1.t_events[0][0]
schritte = int((intervall - starttime) * punkte)
times = np.linspace(starttime, intervall, schritte)
# run through the loop once only, if mit_event = False,
# or no second contact points
else:
params.append([resultat.shape[0], old_spoke, old_x0])
starttime = intervall
print('final message is: ', resultat1.message)
# stack the individual results of the various integrations,
# to get the complete results.
if zaehl_event > 0:
resultat = np.vstack(ergebnis)
print((f'the shape of the total result is {resultat.shape}, '
f'meaning {resultat.shape[0]:,} points in time were considered, '
f'the rhs was called {funktionsaufrufe:,} times.'))
# set these values for the subsequent plots below.
schritte = resultat.shape[0]
times = np.linspace(0., starttime, schritte)
print((f'event was called {zaehl_event}, times and a new contact was '
f' encountered {len(sprungzeit):,} times'))
final message is: The solver successfully reached the end of the integration interval.
the shape of the total result is (6122, 2), meaning 6,122 points in time were considered, the rhs was called 19,108 times.
event was called 11047, times and a new contact was encountered 184 times
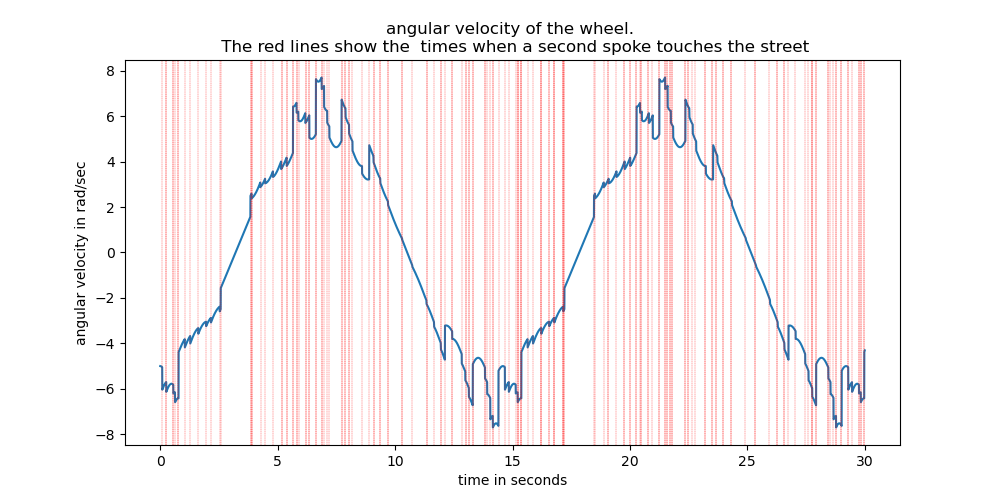
Plot the angular velocity The red lines are where a second contact point is detected.
fig, ax = plt.subplots(1, 1, figsize=(10, 5))
ax.plot(times, resultat[:, 1])
for i in range(len(sprungzeit)):
ax.axvline(sprungzeit[i], color='red', linestyle='--', lw=0.25)
ax.set_xlabel('time in seconds')
ax.set_ylabel('angular velocity in rad/sec')
_ = ax.set_title((f'angular velocity of the wheel. \n The red lines show the '
f' times when a second spoke touches the street'))
Plot the energy of the system
kin_np = np.empty(schritte)
pot_np = np.empty(schritte)
total_np = np.empty(schritte)
zaehler = -1
for i in range(len(ergebnis)):
value = params[i][1] # which spoke is touching the street is stored in params
x0_value = params[i][2] # X coordnate where it touches the street
laenge = params[i][0] # length of ergebnis[i]
pL_vals[-2] = x0_value
pL_vals[-1] = value
for j in range(laenge):
zaehler += 1
kin_np[zaehler] = kin_lam(ergebnis[i][j, 0], ergebnis[i][j, 1],
*pL_vals)[value]
pot_np[zaehler] = pot_lam(ergebnis[i][j, 0], ergebnis[i][j, 1],
*pL_vals)[value]
total_np[zaehler] = kin_np[zaehler] + pot_np[zaehler]
if reibung1 == 0.:
print((f'the deviation ot total energy from being constant is '
f'{(np.max(total_np) - np.min(total_np))/np.max(total_np) *100:.2e}'
f' % of max total energy'))
fig, ax = plt.subplots(1, 1, figsize=(10, 5))
ax.plot(times, kin_np, label='kinetic energy')
ax.plot(times, pot_np, label='potential energy')
ax.plot(times, total_np, label='total energy')
ax.set_title(f'Energy of the wheel, friction = {reibung1}')
ax.set_xlabel('time (sec)')
ax.set_ylabel('energy (Joule)')
_ = ax.legend()
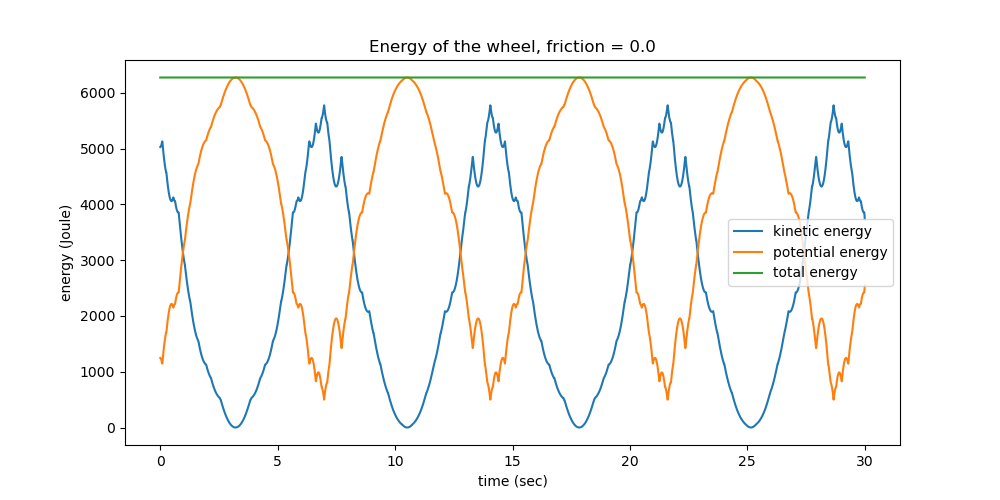
the deviation ot total energy from being constant is 4.78e-09 % of max total energy
Animation¶
Reduce the number of points drawn to around zeitpunkte otherwise it will take a long time to build the animation.
zeitpunkte = 500
# find the coordinates of Dmc and DncEsp.
Dmc_np = np.empty((schritte, 2))
DmcEsp_np = np.empty((schritte, n, 2))
zaehler = -1
for i in range(len(ergebnis)):
value = params[i][1] # which spoke is touching the street is stored in params
x0_value = params[i][2] # X coordnate where it touches the street
laenge = params[i][0] # length of ergebnis[i]
pL_vals[-2] = x0_value
pL_vals[-1] = value
for j in range(laenge):
zaehler += 1
Dmc_np[zaehler] = Dmc_loc_lam(ergebnis[i][j, 0], ergebnis[i][j, 1],
*pL_vals)[value]
DmcEsp_np[zaehler] = [DmcEsp_loc_lam(ergebnis[i][j, 0],
ergebnis[i][j, 1],
*pL_vals)[value][k]
for k in range(n)]
# reduce the number of points of time to around zeitpunkte
times2 = []
Dmc_liste = []
DmcEsp_liste = []
reduction = max(1, int(len(times)/zeitpunkte))
for i in range(len(times)):
if i % reduction == 0:
times2.append(times[i])
Dmc_liste.append(Dmc_np[i])
DmcEsp_liste.append(DmcEsp_np[i])
schritte2 = len(times2)
print(f'animation used {schritte2} points in time')
Dmc_np = np.array(Dmc_liste)
DmcEsp_np = np.array(DmcEsp_liste)
times2 = np.array(times2)
# needed to give the picture the right size.
xmin = np.min(DmcEsp_np[:, :, 0]) - 1
xmax = np.max(DmcEsp_np[:, :, 0]) + 1
ymin = np.min(DmcEsp_np[:, :, 1]) - 1
ymax = np.max(DmcEsp_np[:, :, 1]) + 1
# Data to draw the uneven street
strassex = np.linspace(xmin, xmax, schritte2)
strassey = [gesamt1_lam(strassex[i], amplitude1, frequenz1)
for i in range(schritte2)]
# This is to asign colors of 'plasma' to the spokes
Test = mp.colors.Normalize(0, n)
Farbe = mp.cm.ScalarMappable(Test, cmap='plasma')
farben = [Farbe.to_rgba(l) for l in range(n)] # color of the spokes
if u1 > 0.:
wohin = 'left'
else:
wohin = 'right'
def init_plot():
fig, ax = plt.subplots(figsize=(10, 10), subplot_kw={'aspect': 'equal'})
ax.axis('on')
ax.set_xlim(xmin, xmax)
ax.set_ylim(ymin, ymax)
ax.plot(strassex, strassey) # plot the street
line1, = ax.plot([], [], 'o-', color='black', markersize=10) # center of the wheel
LINE = ['spoke' + str(i) for i in range(n)] # holds the spokes
for i in range(n):
LINE[i], = ax.plot([], [], color=farben[i], lw=2.)
return fig, ax, line1, LINE
fig, ax, line1, LINE = init_plot()
def update(i):
message = (f'running time {times[i]:.2f} sec \n Initial speed is '
f' {np.abs(u1):.2f} radians/sec to the {wohin}')
ax.set_title(message, fontsize=12)
ax.set_xlabel('X direction', fontsize=12)
ax.set_ylabel('Y direction', fontsize=12)
line1.set_data([Dmc_np[i, 0]], [Dmc_np[i, 1]]) # update center of the wheel
for spoke in range(n): # update the spokes
LINE[spoke].set_data([Dmc_np[i, 0], DmcEsp_np[i, spoke, 0]],
[Dmc_np[i, 1], DmcEsp_np[i, spoke, 1]])
return line1, LINE
animation used 511 points in time
Create the animation
fig, ax, line1, LINE = init_plot()
anim = animation.FuncAnimation(fig, update, frames=schritte2,
interval=1250*np.max(times2) / schritte2)
plt.show()