Example Using symjit

Objective

• show how to use symjit as an alternative to lambdify

Explanation

symjit (version 2.4.0 and up) is an alternative to symy’s lambdify. As the usage is slightly different from lambdify, the differences are shown here.

The simulation is a simple 2D pendulum consisting of n links attached to a ceiling.

States

• \(q_{i}\) : The angle of link i w.r.t the inertial frame

• \(u_{i}\) : The angular velocity of link i w.r.t the inertial frame

Parameters

• \(l\) : The length of each link

• \(m\) : The mass of each link

• \(iZZ\) : The moment of inertia of each link around its center of mass

• \(\textrm{reibung}\) : The friction coefficient at each joint

Others

• \(O\) : The inertial frame

• \(PO\) : A point fixed in the inertial frame

• \(A[i]\) : The body fixed frame of link i

• \(Dmc[i]\) : The center of gravity of link i

• \(P[i]\) : The point where frame A[i] joins frame A[i+1]

• \(l\) : The length of the pendulum, that is each link has length = $dfrac{l}{n}$

import sympy as sm
import sympy.physics.mechanics as me
import time
import numpy as np
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt
from symjit import compile_func

Kane’s Equations of Motion

# n = number of links
n = 25
# If term_info is True information about the mass matrix and the force vector
# is printed
term_info = True
plot_energies = True   # if True the energies are plotted
symJIT = True  # If True symjit's compile_func is used, else lambdify

m, g, iZZ, l, reibung = sm.symbols('m, g, iZZ, l, reibung')
q = me.dynamicsymbols(f'q:{n}')
u = me.dynamicsymbols(f'u:{n}')

t = me.dynamicsymbols._t

A = sm.symbols(f'A:{n}', cls=me.ReferenceFrame)
Dmc = sm.symbols(f'Dmc:{n}', cls=me.Point)
P = sm.symbols(f'P:{n}', cls=me.Point)
rhs = list(sm.symbols(f'rhs:{n}'))

O = me.ReferenceFrame('O')
PO = me.Point('PO')
PO.set_vel(O, 0)

l1 = l/n
l2 = l/(2 * n)

A[0].orient_axis(O, q[0], O.z)
A[0].set_ang_vel(O, u[0] * O.z)

Dmc[0].set_pos(PO, l2*A[0].x)
Dmc[0].v2pt_theory(PO, O, A[0])
P[0].set_pos(PO, l1*A[0].x)
P[0].v2pt_theory(PO, O, A[0])

for i in range(1, n):
    A[i].orient_axis(O, q[i], O.z)
    A[i].set_ang_vel(O, u[i] * O.z)

    Dmc[i].set_pos(P[i-1], l2*A[i].x)
    Dmc[i].v2pt_theory(P[i-1], O, A[i])
    P[i].set_pos(P[i-1], l1*A[i].x)
    P[i].v2pt_theory(P[i-1], O, A[i])

BODY = []
for i in range(n):
    inertia = me.inertia(A[i], 0., 0., iZZ)
    body = me.RigidBody('body' + str(i), Dmc[i], A[i], m, (inertia, Dmc[i]))
    BODY.append(body)

FL1 = [(Dmc[i], -m*g*O.y) for i in range(n)]
Torque = [(A[i], - u[i] * reibung * A[i].z) for i in range(n)]
FL = FL1 + Torque

kd = [u[i] - q[i].diff(t) for i in range(n)]

KM = me.KanesMethod(O, q_ind=q, u_ind=u, kd_eqs=kd)
(fr, frstar) = KM.kanes_equations(BODY, FL)

MM = KM.mass_matrix_full
if term_info:
    print('MM DS', me.find_dynamicsymbols(MM))
    print('MM free symbols', MM.free_symbols)
    print(f'MM contains {sm.count_ops(MM):,} operations, '
          f'{sm.count_ops(sm.cse(MM)):,} after cse', '\n')

force = KM.forcing_full
if term_info:
    print('force DS', me.find_dynamicsymbols(force))
    print('force free symbols', force.free_symbols)
    print(f'force contains {sm.count_ops(force):,} operations '
          f'{sm.count_ops(sm.cse(force)):,} after cse', '\n')

MM DS {q19(t), q0(t), q23(t), q20(t), q5(t), q13(t), q11(t), q7(t), q22(t), q2(t), q3(t), q14(t), q15(t), q10(t), q16(t), q6(t), q8(t), q24(t), q9(t), q21(t), q18(t), q12(t), q1(t), q17(t), q4(t)}
MM free symbols {l, m, t, iZZ}
MM contains 9,606 operations, 1,394 after cse

force DS {q19(t), u18(t), q23(t), u14(t), u10(t), u13(t), u24(t), q3(t), u12(t), u19(t), u2(t), q16(t), q15(t), q10(t), q8(t), q6(t), u3(t), u16(t), u4(t), q9(t), u9(t), q18(t), u21(t), u1(t), u8(t), q17(t), q4(t), q0(t), q20(t), q5(t), u5(t), u23(t), q11(t), q22(t), q7(t), u20(t), q2(t), u11(t), q14(t), u0(t), u15(t), u7(t), u6(t), u17(t), q21(t), u22(t), q13(t), q12(t), q1(t), q24(t)}
force free symbols {g, l, m, t, reibung}
force contains 12,156 operations 2,721 after cse

Functions for the kinetic and the potential energies. Always useful to detect mistakes.

Using sm.lambdify(…)

if plot_energies and not symJIT:
    qL = q + u
    pL = [m, g, l, iZZ, reibung]

    kin_energie = sum([koerper.kinetic_energy(O) for koerper in BODY])
    pot_energie = sum([m*g*me.dot(koerper.pos_from(PO), O.y)
                       for koerper in Dmc])
    kin_lam = sm.lambdify(qL + pL, kin_energie, cse=True)
    pot_lam = sm.lambdify(qL + pL, pot_energie, cse=True)
else:
    pass

using symjit.compile_func(..)

As symjit does not accept dynamicsymbols -which are needed with Kane’s method- they must be substituted with sympy symbols.

if plot_energies and symJIT:
    w1 = sm.symbols(f'w:{n}')
    v1 = sm.symbols(f'v:{n}')
    dict_w = {q[i]: w1[i] for i in range(n)}
    dict_v = {u[i]: v1[i] for i in range(n)}

    kin_energie = me.msubs(sum([koerper.kinetic_energy(O)
                                for koerper in BODY]), dict_w, dict_v)
    pot_energie = me.msubs(sum([m*g*me.dot(koerper.pos_from(PO), O.y)
                                for koerper in Dmc]), dict_w, dict_v)
    kin_jit = compile_func((*w1, *v1), kin_energie, params=(m, g, l, iZZ,
                                                            reibung))
    pot_jit = compile_func((*w1, *v1), pot_energie, params=(m, g, l, iZZ,
                                                            reibung))
else:
    pass

Use symjit.

As MM and force are sympy matrices, they must be converted into lists. As symjit does not accept dynamicsymbols -which are needed to form the equations of motion- they must be substituted with sympy symbols.

if symJIT:
    start3 = time.time()
    w1 = sm.symbols(f'w:{n}')
    v1 = sm.symbols(f'v:{n}')
    dict_w = {q[i]: w1[i] for i in range(n)}
    dict_v = {u[i]: v1[i] for i in range(n)}
    MM1 = me.msubs(MM, dict_w, dict_v)
    force1 = me.msubs(force, dict_w, dict_v)
    MM1 = [MM1[i, j] for i in range(MM1.shape[0]) for j in range(MM1.shape[1])]
    force1 = list(force1)
    pL1 = (m, g, l, iZZ, reibung)
    MM_jit = compile_func((*w1, *v1), MM1, params=pL1)
    force_jit = compile_func((*w1, *v1), force1, params=pL1)

    print(f'it took {time.time()-start3:.3f} sec to do compile_func')

else:
    pass

it took 0.216 sec to do compile_func

Use lambdify

if not symJIT:
    start3 = time.time()
    qL = q + u
    pL = [m, g, l, iZZ, reibung]

    MM_lam = sm.lambdify(qL + pL, MM, cse=True)
    force_lam = sm.lambdify(qL + pL, force, cse=True)

    print(f'it took {time.time()-start3:.3f} sec to do the lambdification')
else:
    pass

Numerical Integration

# method='Radau' in solve_ivp gives a more constant total energy if
# $reibung = 0.$

# Input variables
m1 = 1.
g1 = 9.8
l1 = 20
reibung1 = 0.

q1 = [3.*np.pi/2. + np.pi * i / n for i in range(1, n+1)]
u1 = [0. for _ in range(n)]

intervall = 10.0
punkte = 50

schritte = int(intervall * punkte)
times = np.linspace(0., intervall, schritte)
t_span = (0., intervall)

iZZ1 = 1./12. * m1 * (l1/n)**2        # from the internet

pL_vals = [m1, g1, l1, iZZ1, reibung1]
y0 = [*q1, *u1]

if symJIT is False:

    def gradient(t, y, args):
        sol = np.linalg.solve(MM_lam(*y, *args), force_lam(*y, *args))
        return np.array(sol).T[0]


else:

    def gradient(t, y, args):
        # The list must be reshaped to a matrix.
        MM_matrix = np.array(MM_jit(*y, *args)).reshape((n*2, n*2))
        force_vector = np.array(force_jit(*y, *args))
        sol = np.linalg.solve(MM_matrix, force_vector)
        return np.array(sol)

start2 = time.time()
resultat1 = solve_ivp(gradient, t_span, y0, t_eval=times, args=(pL_vals,),
                      method='Radau')
end2 = time.time()

resultat = resultat1.y.T
print('resultat shape', resultat.shape)
print(resultat1.message, '\n')

if symJIT:
    msg = 'used symjit'
else:
    msg = 'used lambdify'
print(f"To numerically integrate an intervall of {intervall} sec the "
      f"routine cycled {resultat1.nfev:,} times and it took "
      f"{end2 - start2:.3f} sec, {msg} ")

resultat shape (500, 50)
The solver successfully reached the end of the integration interval.

To numerically integrate an intervall of 10.0 sec the routine cycled 10,083 times and it took 3.426 sec, used symjit

Plot the Energies

if plot_energies:
    kin_np = np.empty(schritte)
    pot_np = np.empty(schritte)
    total_np = np.empty(schritte)

    for i in range(schritte):
        if symJIT is False:
            kin_np[i] = kin_lam(*[resultat[i, j]
                                  for j in range(resultat.shape[1])], *pL_vals)
            pot_np[i] = pot_lam(*[resultat[i, j]
                                  for j in range(resultat.shape[1])], *pL_vals)
            total_np[i] = kin_np[i] + pot_np[i]
        else:
            kin_np[i] = kin_jit(*[resultat[i, j]
                                  for j in range(resultat.shape[1])], *pL_vals)
            pot_np[i] = pot_jit(*[resultat[i, j]
                                  for j in range(resultat.shape[1])], *pL_vals)
            total_np[i] = kin_np[i] + pot_np[i]

    if reibung1 == 0.:
        max_total = np.max(np.abs(total_np))
        min_total = np.min(np.abs(total_np))
        delta = max_total - min_total
        print(f'max deviation of total energy from constant is '
              f'{delta/max_total * 100:.3e} % of max. total energy')
    fig, ax = plt.subplots(figsize=(10, 5))
    for i, j in zip((kin_np, pot_np, total_np),
                    ('kinetic energy', 'potential energy', 'total energy')):
        ax.plot(times, i, label=j)
    ax.set_title("Energies of the system")
    ax.set_xlabel('time (sec)')
    ax.set_ylabel('energy (Nm)')
    _ = ax.legend()
else:
    pass

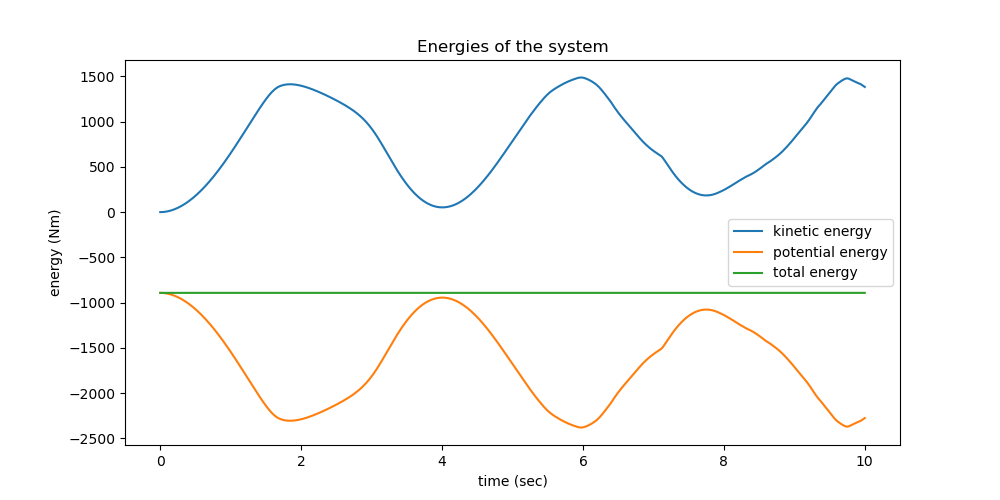
max deviation of total energy from constant is 3.108e-02 % of max. total energy