Zermelo’s Problem (betts-10-148)

This is example 10.148 from John T. Betts, Practical Methods for Optimal Control Using NonlinearProgramming, 3rd edition, Chapter 10: Test Problems. The goal is to minimize the final time \(t_f\) to reach the point (0 / 0), having started at the point (3.5 / -1.8).

More information about Zermelo’s navigation problem can be found at https://en.wikipedia.org/wiki/Zermelo%27s_navigation_problem

States

• \(x, y\) : state variables

Controls

• \(\theta\) : control variable

import numpy as np
import sympy as sm
import sympy.physics.mechanics as me
import time
from opty import Problem
from opty.utils import MathJaxRepr

Equations of motion.

t = me.dynamicsymbols._t

x, y = me.dynamicsymbols('x, y')
theta = me.dynamicsymbols('theta')
h = sm.symbols('h')
V, c = sm.symbols('V, c')

eom = sm.Matrix([
    -x.diff(t) + V*sm.cos(theta) + c*y,
    -y.diff(t) + V*sm.sin(theta),
])

MathJaxRepr(eom)

$$\left[\begin{matrix}V \cos{\left(\theta \right)} + c y - \dot{x}\\V \sin{\left(\theta \right)} - \dot{y}\end{matrix}\right]$$

Define and Solve the Optimization Problem

num_nodes = 2001
t0 = 0*h
tf = (num_nodes - 1) * h
interval_value = h

state_symbols = (x, y)
unkonwn_input_trajectories = (theta, )

par_map = {V: 1.0, c: -1.0}

Specify the objective function and form the gradient.

def obj(free):
    return free[-1]


def obj_grad(free):
    grad = np.zeros_like(free)
    grad[-1] = 1.0
    return grad

Set the instance constraints. Forcing \(h \geq 0\) will avoid physically meaninigless negative time intervals.

instance_constraints = (
    x.func(t0) - 3.5,
    y.func(t0) + 1.8,
    x.func(tf),
    y.func(tf),
)

bounds = {
        h: (0.0, 0.5),
}

Create the optimization problem and set any options.

prob = Problem(
    obj,
    obj_grad,
    eom,
    state_symbols,
    num_nodes,
    interval_value,
    instance_constraints=instance_constraints,
    known_parameter_map=par_map,
    bounds=bounds,
    time_symbol=t,
)

Give some rough estimates for the trajectories.

initial_guess = np.ones(prob.num_free) * 0.1

Find the optimal solution.

start_time = time.time()
solution, info = prob.solve(initial_guess)
end_time = time.time()
print(f"Solving time: {end_time - start_time:.2f} seconds")
print(info['status_msg'])
Jstar = 5.26493205
print(f"Objective value achieved: {(num_nodes-1)*info['obj_val']:.4f} ",
      f"as per the book it is {Jstar:.4f}, so the error is: "
      f"{((num_nodes-1)*info['obj_val'] - Jstar)/Jstar*100:.3f} % ")

Solving time: 3.42 seconds
b'Algorithm terminated successfully at a locally optimal point, satisfying the convergence tolerances (can be specified by options).'
Objective value achieved: 5.2637  as per the book it is 5.2649, so the error is: -0.023 %

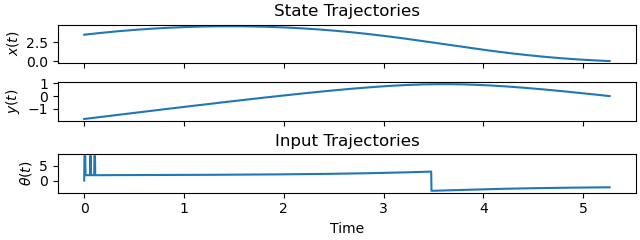
Plot the optimal state and input trajectories.

_ = prob.plot_trajectories(solution)

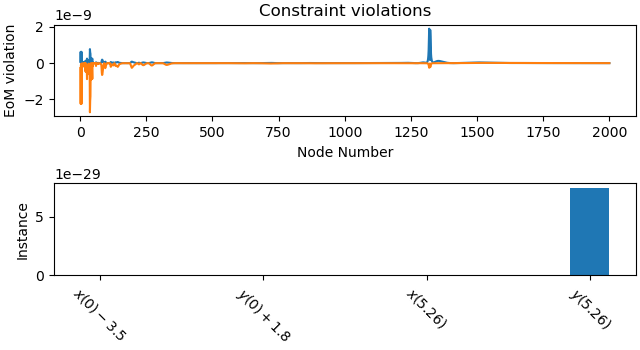
Plot the constraint violations.

_ = prob.plot_constraint_violations(solution)

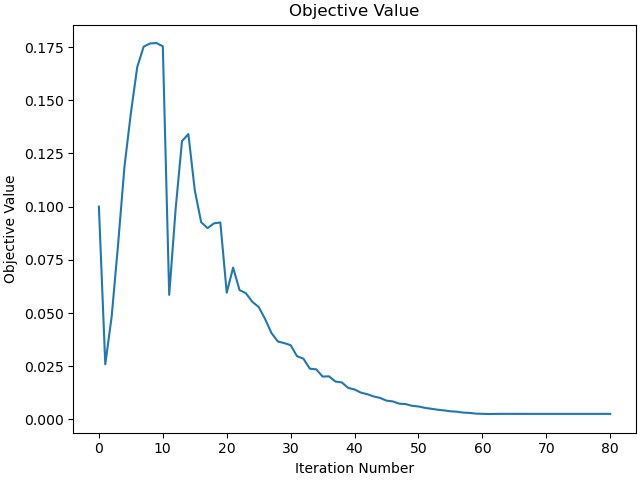
Plot the objective function as a function of optimizer iteration.

_ = prob.plot_objective_value()